
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=![]() ∠BAC.
∠BAC.
其中正确的结论有( )

A.2个 B.3个 C.4个 D.5个
【答案】C
【解析】
试题分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EAC=∠ABC+∠ACB=2∠ABC,根据角平分线的定义可得∠EAC=2∠EAD,然后求出∠EAD=∠ABC,再根据同位角相等,两直线平行可得AD∥BC,判断出①正确;
根据两直线平行,内错角相等可得∠ADB=∠CBD,再根据角平分线的定义可得∠ABC=2∠CBD,从而得到∠ACB=2∠ADB,判断出②正确;
根据两直线平行,内错角相等可得∠ADC=∠DCF,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义整理可得∠ADC=90°﹣∠ABD,判断出③正确;
根据三角形的外角性质与角平分线的定义表示出∠DCF,然后整理得到∠BDC=![]() ∠BAC,判断出⑤正确,再根据两直线平行,内错角相等可得∠CBD=∠ADB,∠ABC与∠BAC不一定相等,所以∠ADB与∠BDC不一定相等,判断出④错误.
∠BAC,判断出⑤正确,再根据两直线平行,内错角相等可得∠CBD=∠ADB,∠ABC与∠BAC不一定相等,所以∠ADB与∠BDC不一定相等,判断出④错误.
解:由三角形的外角性质得,∠EAC=∠ABC+∠ACB=2∠ABC,
∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD,
∴∠EAD=∠ABC,
∴AD∥BC,故①正确,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABC=2∠CBD,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,故②正确;
∵AD∥BC,
∴∠ADC=∠DCF,
∵CD是∠ACF的平分线,
∴∠ADC=![]() ∠ACF=
∠ACF=![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)=![]() (180°﹣∠ACB)=
(180°﹣∠ACB)=![]() (180°﹣∠ABC)=90°﹣∠ABD,故③正确;
(180°﹣∠ABC)=90°﹣∠ABD,故③正确;
由三角形的外角性质得,∠ACF=∠ABC+∠BAC,∠DCF=∠BDC+∠DBC,
∵BD平分∠ABC,CD平分∠ACF,
∴∠DBC=![]() ∠ABC,∠DCF=
∠ABC,∠DCF=![]() ∠ACF,
∠ACF,
∴∠BDC+∠DBC=![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)=![]() ∠ABC+
∠ABC+![]() ∠BAC=∠DBC+
∠BAC=∠DBC+![]() ∠BAC,
∠BAC,
∴∠BDC=![]() ∠BAC,故⑤正确;
∠BAC,故⑤正确;
∵AD∥BC,
∴∠CBD=∠ADB,
∵∠ABC与∠BAC不一定相等,
∴∠ADB与∠BDC不一定相等,
∴BD平分∠ADC不一定成立,故④错误;
综上所述,结论正确的是①②③⑤共4个.
故选C.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2-x-2=0可通过因式分解化为(x-2)(x+1)=0,由基本事实得x-2=0或x+1=0,即方程的解为x=2或x=-1.
(1)、试利用上述基本事实,解方程:2x2-x=0:
(2)、若(x2+y2)(x2+y2-1)-2=0,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列说法:①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内.正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N, 有下列四个结论:① DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF. 其中,正确的结论有( )
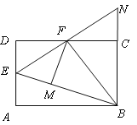
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com