
【题目】如图,点A、B坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,t= ;
(2)当t=4时,直接写出S的值;
(3)求出S与t的函数关系式;
(4)若S=12,则t= .

【答案】(1)t=![]() (2) 7(3)
(2) 7(3) (4)8
(4)8
【解析】试题分析:(1)证明△BCD∽△BOA,利用线段比求出t值.(2)当t=4时,点E与A重合,证明△CBF∽△OBA求出CF.(3)根据t的取值范围求出S的值.(4) 由题意可知把S=12代入S=![]()
![]() t2+2t中,
t2+2t中, ![]()
![]() t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)
t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)![]() 当S=12时,t=8.
当S=12时,t=8.
试题解析:
(1)由题意可得∠BCD=∠BOA=90°,∠CBD=∠OBA,
∴△BCD∽△BOA,
∴![]()
而CD=OE=t,BC=8CO=8![]() ,OA=4,
,OA=4,
则8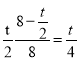 ,解得t=
,解得t=![]() ,
,
∴当点D在直线AB上时,t=![]() .
.
(2)(2)当t=4时,点E与A重合,设CD与AB交于点F,
则由△CBF∽△OBA得![]() ,
,
即![]() ,解得CF=3,
,解得CF=3,
∴S=![]() OC(OE+CF)=
OC(OE+CF)=![]() ×2×(3+4)=7.
×2×(3+4)=7.
(3)![]() 当0<t≤
当0<t≤![]() 时,S=
时,S=![]() t2,
t2,
![]() 当
当![]() <t≤4时,如图(2),
<t≤4时,如图(2),

∵A(4,0),B(0,8)
∴直线AB的解析式为y=-2x+8,G(t, ![]() 2t+8),F(4
2t+8),F(4![]()
![]() ,
,![]() ),
),
∴DF=![]()
![]() 4,DG=
4,DG=![]()
![]() 8,
8,
∴S=S矩形COED-S△DFG=t×![]()
![]()
![]() (
(![]()
4)( ![]()
![]() 8)
8)
=-![]() t2+10t-16.
t2+10t-16.

![]() 当
当![]() 时,如图(3)
时,如图(3)
由∠BFC=∠BAO tan∠BAO=tan∠BFC
![]() =2
=2 ![]()
∴S=S△BOA![]() S△BCF=
S△BCF=![]() ×4×8
×4×8![]()
![]() ×(4
×(4![]() -
-![]() )(8
)(8![]()
![]() =
=![]()
![]() t2+2t.
t2+2t.
综上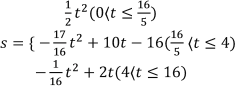 (4)8
(4)8
(提示:由题意可知把S=12代入S=![]()
![]() t2+2t中,
t2+2t中, ![]()
![]() . t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)
. t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)![]() 当S=12时,t=8.)
当S=12时,t=8.)
点睛: 本题考查的是二次函数的综合运用,相似三角形的判定以及考生的做题能力,解题时要注意分段函数.


科目:初中数学 来源: 题型:
【题目】东营市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收1.5元(不足1千米按1千米计).某人从甲地到乙地经过的路程是x千米,出租车费为15.5元,那么x的最大值是( )
A. 11 B. 8 C. 7 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①在2和3之间只有 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 这四个无理数;②数轴上的点与有理数一一对应;③绝对值等于本身的数是0;④0除以任何数都得0;⑤近似数7.30所表示的准确数a的范围是:7.295≤a<7.305.其中正确的个数是( )
这四个无理数;②数轴上的点与有理数一一对应;③绝对值等于本身的数是0;④0除以任何数都得0;⑤近似数7.30所表示的准确数a的范围是:7.295≤a<7.305.其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H. 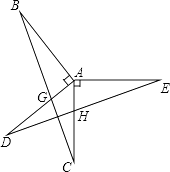
求证:
(1)△ABC≌△ADE;
(2)BC⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识背景】在学习计算框图时,可以用“ ![]() ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ![]() ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ![]() ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) 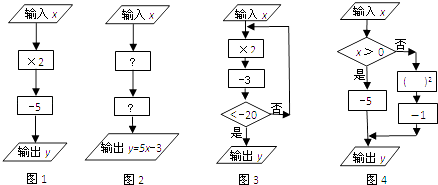
【尝试解决】
(1)①如图1,当输入数x=﹣2时,输出数y=;
②如图2,第一个“ ![]() ”内,应填; 第二个“
”内,应填; 第二个“ ![]() ”内,应填;
”内,应填;
(2)①如图3,当输入数x=﹣1时,输出数y=;②如图4,当输出的值y=17,则输入的值x=;
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量x,输出数为水费y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com