
 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=6cm,CD=12cm,则图中阴影部分的面积是
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=6cm,CD=12cm,则图中阴影部分的面积是



 (π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB),求出OF′⊥AB,由垂径定理求出AF′=BF′=3cm,代入即可得出答案.
(π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB),求出OF′⊥AB,由垂径定理求出AF′=BF′=3cm,代入即可得出答案.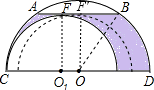 将⊙O1移动到O1与O重合,则F和F′重合,连接OB,AO,
将⊙O1移动到O1与O重合,则F和F′重合,连接OB,AO, CD=6cm,
CD=6cm, OB,
OB, cm,
cm, (π×OB2-π×OF′2)-(S扇形AOB-S△AOB)
(π×OB2-π×OF′2)-(S扇形AOB-S△AOB) π×(OB2-OF′2)-
π×(OB2-OF′2)- +
+ ×6×3
×6×3
 π×BF′2-6π+9
π×BF′2-6π+9
 π×9-6π+9
π×9-6π+9
 -
- π)cm2.
π)cm2. (π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB)=
(π×OB2-π×OF′2)-(S扇形AOB-S三角形AOB)= π×BF′2-(S扇形AOB-S三角形AOB),题目比较典型,是一道比较好的题目.
π×BF′2-(S扇形AOB-S三角形AOB),题目比较典型,是一道比较好的题目. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com