
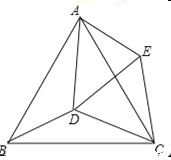
【题目】如图,已知等边△ABC,点D为△ABC内一点,连接DA、DB、DC,∠ADB=120°.以CD为边向CD上方作等边△CDE,连接AE.(0°<∠ACE<60°)
(1)求证:△BDC≌△AEC;
(2)若DA=![]() +1,DB=
+1,DB=![]() ﹣1,DC=2n(n为大于1的整数),求∠BDC的度数;
﹣1,DC=2n(n为大于1的整数),求∠BDC的度数;
(3)若△ADE为等腰三角形,求![]() 的值.
的值.
【答案】(1)证明详见解析;(2)150°;(3)![]() .
.
【解析】
试题分析:(1)由等边三角形的性质得出结论,直接用SAS得出结论;
(2)用等边三角形的性质得出DE=CD,进而判断出△ADE是直角三角形,即可得出结论;
(3)分三种情况先判断出△ADE是等边三角形,进而构造出直角三角形,用含30°的直角三角形的性质得出结论即可.
试题解析:(1)∵△ABC和△CDE是等边三角形,
∴BC=AC,CD=CE=DE,∠ACB=∠DCE=∠CED=60°,
∴∠BCD=∠ACE,
在△BDC和△AEC中,
BC=AC,∠BCD=∠ACE,CE=CE,
∴△BDC≌△AEC(SAS);
(2)由(1)知,DE=CD=2n,△BDC≌△AEC,
∴∠BDC=∠AEC,AE=BD=![]() ﹣1,
﹣1,
∵DA=![]() +1,AE=
+1,AE=![]() ﹣1,DE=2n,
﹣1,DE=2n,
∴![]() =
=![]() =
=![]() ,
,
∴△ADE是直角三角形,
∴∠AED=90°,
∴∠BDC=∠AEC=∠AED+∠CED=150°;
(3)如图,
①当AD=AE时,由(1)知,△BDC≌△AEC,
∴∠CAE=∠CBD,AE=BD,
∴AD=BD,
∵∠ADB=120°,
∴∠BAD=∠ABD=30°,
∵∠ABC=∠BAC=60°,
∴∠CBD=∠CAD=∠CAE=30°,
∴∠DAE=60°,
∴△ADE是等边三角形;
②当AD=DE时,∵CD=DE,
∴AD=CD,
∴∠CAD=∠DCA,
∵∠BAC=∠BCA,
∴∠BAD=∠BCD,
在△ABD和△CBD中,
AB=BC,∠BAD=∠BCD,AD=CD,
∴△ABD≌△CBD,
∴∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
以后同①的方法得出,△ADE是等边三角形,
③当AE=DE时,同②的方法得出,△ADE是等边三角形,
即:△ADE是等边三角形
过点D作DF⊥BC,
∴BC=2CF,在Rt△CDF中,∠DCF=30°,
∴cos30°=![]() ,
,
∴![]() =
=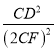 =
=![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
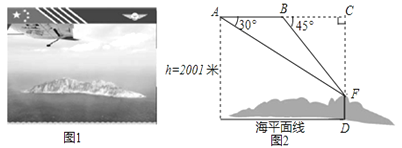
【题目】国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得峰顶F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度是多少米.(结果保留整数,参考数值:![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是假命题的是( )
A.两点之间,线段最短
B.过一点有且只有一条直线与已知直线垂直
C.直角三角形的两个锐角互余
D.两条直线被第三条直线所截,同位角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
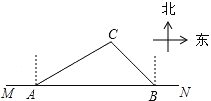
【题目】2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com