
分析 (1)根据方程的系数结合根的判别式即可得出△=(a-4)2≥0,此题得证;
(2)利用因式分解法解一元二次方程即可得出方程的两个根,结合该方程的两个根为连续的偶数即可得出关于a的一元一次方程,解之即可得出结论.
解答 (1)证明:在方程x2-ax+2a-4=0中,△=a2-4(2a-4)=a2-8a+16=(a-4)2,
∵(a-4)2≥0,
∴不论a取何实数,该方程都有实数根;
(2)解:∵x2-ax+2a-4=(x-2)(x-a+2)=0,
解得:x1=2,x2=a-2,
∵两个根为连续的偶数,
∴x2=a-2=0或4,
∴a=2或6.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,利用因式分解法解出方程的两个根为x1=2、x2=a-2是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图所示,船A和船B同时从小岛O出发,船A沿北偏西20°的方向航行,船B沿北偏东70°的方向航行.
如图所示,船A和船B同时从小岛O出发,船A沿北偏西20°的方向航行,船B沿北偏东70°的方向航行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
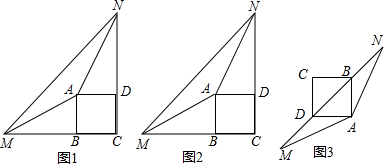
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC.
已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com