
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 . 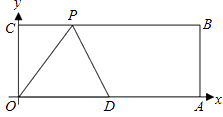
【答案】(2,4)或(3,4)或(8,4)
【解析】解:当OD=PD(P在右边)时,根据题意画出图形,如图所示:
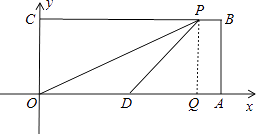
过P作PQ⊥x轴交x轴于Q,在直角三角形DPQ中,PQ=4,PD=OD= ![]() OA=5,
OA=5,
根据勾股定理得:DQ=3,故OQ=OD+DQ=5+3=8,则P1(8,4);
当PD=OD(P在左边)时,根据题意画出图形,如图所示:
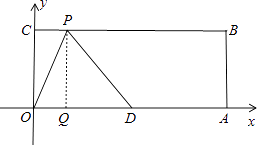
过P作PQ⊥x轴交x轴于Q,在直角三角形DPQ中,PQ=4,PD=OD=5,
根据勾股定理得:QD=3,故OQ=OD﹣QD=5﹣3=2,则P2(2,4);
当PO=OD时,根据题意画出图形,如图所示:

过P作PQ⊥x轴交x轴于Q,在直角三角形OPQ中,OP=OD=5,PQ=4,
根据勾股定理得:OQ=3,则P3(3,4),
综上,满足题意的P坐标为(2,4)或(3,4)或(8,4).
所以答案是:(2,4)或(3,4)或(8,4)
【考点精析】根据题目的已知条件,利用等腰三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】已知四个数:a=![]() b=- (-3) , c= -(-1)2019, d=
b=- (-3) , c= -(-1)2019, d=![]() .
.
(1) 化简a,b,c,d 得a= ,b= ,c= ,d= ;
(2) 把这四个数在数轴上分别表示出来:

(3)用“<”把 a,b,c,d 连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
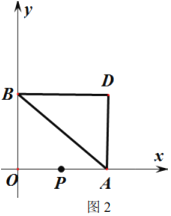
【题目】如图1,在平面直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() 分别在
分别在![]() 轴正半轴和
轴正半轴和![]() 轴正半轴上,且
轴正半轴上,且![]() ,点
,点![]() 从原点出发以每秒
从原点出发以每秒![]() 个单位长度的速度沿x轴正半轴方向运动.
个单位长度的速度沿x轴正半轴方向运动.

(1)求点![]() 的坐标.
的坐标.
(2)连接![]() 设三角形
设三角形![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() 并直接写出
并直接写出![]() 的取值范围.
的取值范围.
(3)当点![]() 在
在![]() 上运动时,将线段
上运动时,将线段![]() 沿
沿![]() 轴正方向平移,使点
轴正方向平移,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() ,将线段
,将线段![]() 沿
沿![]() 轴正方向平移,使点
轴正方向平移,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,取
,取![]() 的中点
的中点![]() 是否存在
是否存在![]() 的值,使三角形
的值,使三角形![]() 的面积等于三角形
的面积等于三角形![]() 的面积?若存在,求出
的面积?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: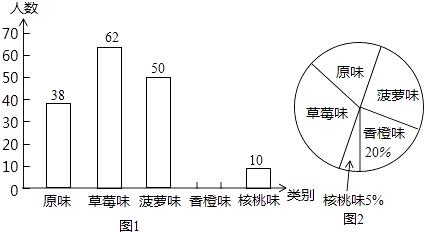
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学化简代数式a+2+ ![]() 的过程,请仔细阅读并解答所提出的问题. a+2+
的过程,请仔细阅读并解答所提出的问题. a+2+ ![]() =2+a+
=2+a+ ![]() …第一步
…第一步
=(2+a)(2﹣a)+a2…第二步
=2﹣a2+a2…第三步
=2…第四步
(1)小明的解法从第步开始出现错误,正确的化简结果是;
(2)原代数式的值能等于2吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.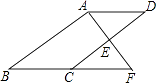
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com