

分析 (1)根据题意作出合适的辅助线,然后根据锐角三角函数即可求得AC的长;
(2)根据题意和锐角三角函数可以求得小明所乘坐的小船走的距离.
解答 解:(1)作CD⊥BA交BA的延长线于点D,
由题意可得,BC=120米,∠CBD=30°,
则CD=60米,
∵∠DCA=30°,
∴AC=$\frac{CD}{cos30°}=\frac{60}{\frac{\sqrt{3}}{2}}=40\sqrt{3}$米,
即此时点A到点C的距离是40$\sqrt{3}$米;
(2)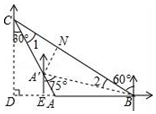 作A′N⊥BC于点N,作A′E⊥BA交BA的延长线于点E,
作A′N⊥BC于点N,作A′E⊥BA交BA的延长线于点E,
由题意可得,
∠1=30°,∠EA′B=′75°,∠EA′A=30°,∠CBD=30°,
则∠AA′B=45°,
∴∠2=15°,
∴∠A′BE=15°,
∴A′N=A′E,
设AA′=x,
则A′E=$\frac{\sqrt{3}x}{2}$,
∴A′N=$\frac{\sqrt{3}x}{2}$,
∴CA′=$\sqrt{3}x$,
∵CA=$40\sqrt{3}$,
∴x+$\sqrt{3}$x=40$\sqrt{3}$,
得x=$20\sqrt{3}-20$
答:此时小明所乘坐的小船走的距离是($20\sqrt{3}-20$)米.
点评 本题考查解直角三角形的应用-方向角问题、勾股定理的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数和数形结合的思想解答.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(-1,3),B(-3,1),C(-1,1).请解答下列问题:
如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(-1,3),B(-3,1),C(-1,1).请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △OAB是⊙O的内接三角形,∠AOB=120°,过O作OE⊥AB于点E,交⊙O于点C,延长OB至点D,使OB=BD,连CD.
△OAB是⊙O的内接三角形,∠AOB=120°,过O作OE⊥AB于点E,交⊙O于点C,延长OB至点D,使OB=BD,连CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
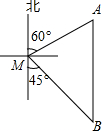 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com