练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

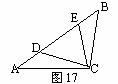
    如图17，在Rt△ABC中，∠ACB=90°，AC=AE，BC=BD，则∠ACD+∠BCE=______．

    ．解一：如图25，设∠ACD=∠1，∠BCE=∠2，∠DCE=∠3．∵AC=AE，∴∠AEC=∠1+∠3．

    ∵BC=BD，∴∠BDC=∠2+∠3．

    两式相加得∠AEC+∠BDC=(∠1+∠2+∠3)+∠3=90°+∠3．

    又在△DCE中∠DEC+∠EDC+∠3=180°．∴90°+2∠3=180°,∠3=45°，∴∠1+∠2=45°．

    解二：∵∠ACE是等腰△ACE的底角，∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

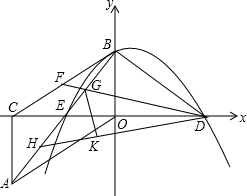    如图，Rt△AOC中，∠ACO=90°，∠AOC=30°．将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO，BO、CO恰好分别在y轴、x轴上．再将Rt△BCO沿y轴对折得到Rt△BDO．取BC中点F，连接DF，交AB于点G，将△BDG沿DF对折得到△KDG．直线DK交AB于点H．
    （1）填空：CE：ED=
    1：3
    1：3
    ，AB：AC=
    		7
    ：1
    		7
    ：1
    ；
    （2）若BH=
    10
    		21
    7
    ，求直线BD解析式；
    （3）在（2）的条件下，一抛物线过点D、点E、点B，此抛物线位于直线BD上方有一动点Q，△BDQ的面积有无最大值？若有，请求出点Q的坐标；若无，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图：已知M是Rt△ABC的斜边BC的中点，P、Q分别在AB、AC上且BP=5，CQ=3，PM⊥QM，则PQ为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点

    ⑴如图②，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．

    ⑵在△ABC中，∠A＜∠B＜∠C．

    ①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；

    ②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．

    【根据2011江津市中考试第17题改编】

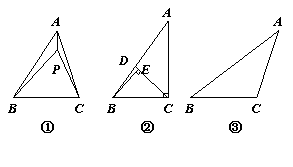
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图17，Rt△ACB中，∠ABC＝90°，点D、E在AB上，AC＝AD，BE＝BC，则∠DCE的大小是________

    .

    查看答案和解析>>

    同步练习册答案