
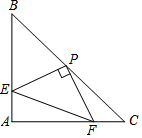
 ��ͼ����֪��ABC��AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC��E��F����������������ۣ���EF=CP����CF=AE����2PF2=EF2���ܡ�AEP+��AFP=180�㣻�ݵ���EPF�ڡ�ABC���ƶ���P��תʱ����E����A��B�غϣ���S�ı���AEPF=$\frac{1}{2}$S��ABC������������ʼ����ȷ���У�������
��ͼ����֪��ABC��AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC��E��F����������������ۣ���EF=CP����CF=AE����2PF2=EF2���ܡ�AEP+��AFP=180�㣻�ݵ���EPF�ڡ�ABC���ƶ���P��תʱ����E����A��B�غϣ���S�ı���AEPF=$\frac{1}{2}$S��ABC������������ʼ����ȷ���У�������| A�� | �٢ڢۢܢ� | B�� | �٢ڢ� | C�� | �٢ۢܢ� | D�� | �ڢۢܢ� |
���� �ٴ���EPF�Ƶ�P��ת�����У�PE�ij����DZ仯�ģ�����EF�ij��ȵı仯�ģ���PC�Dz���ģ��ʢٴ���
�ڢۢ���ȷ��ֻҪ֤����EPA�ա�FPC�����ɽ�����⣮
����ȷ��ֻҪ֤����PEF�ǵ���ֱ�������μ��ɣ�
��� �⣺��ͼ������AP��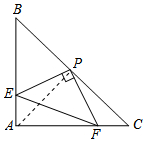
��AB=AC����BAC=90�㣬PB=PC��
��PA=PB=PC��AP��BC��
���PAB=��C=45�㣬
���APC=��EPF=90�㣬
���EPA=��FPC��
�ڡ�EPA�͡�FPC�У�
$\left\{\begin{array}{l}{��EAP=��C}\\{AP=PC}\\{��EPA=��FPC}\end{array}\right.$��
���EPA�ա�FPC��
��AE=CF��PE=PF���ʢ���ȷ��S��EPA=S��FPC��
���PEF�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$PF��
��EF2=2PF2���ʢ���ȷ��
��S�ı���AEPF=S��PAE+S��PAF=S��PFC+S��PAF=S��APC=$\frac{1}{2}$S��ABC���ʢ���ȷ��
�ߡ�EAF+��EPF=180�㣬
���AEP+��AFP=360��-����EAF-��EPF��=180�㣬�ʢ���ȷ��
�ߡ�EPF�Ƶ�P��ת�����У�PE�ij����DZ仯�ģ�
��EF�ij��ȵı仯�ģ���PC�Dz���ģ��ʢٴ���
��ѡD��
���� ���⿼�����ֱ�������ε����ʡ�ȫ�������ε��ж������ʡ��ı��ε���������ɶ�����֪ʶ������Ĺؼ�����ȷѰ��ȫ�������ν�����⣬ѧ�����ӳ��ø����ߣ������п��������ͣ�


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 2��-4 | C�� | -4 | D�� | ��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��1�� | B�� | ��2��-1�� | C�� | ��2��1�� | D�� | ��-2��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
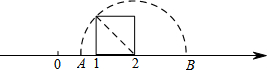 ��ͼ��������ĵ�λ�����߶�Ϊ����һ�������Σ��Ա�ʾ��2�ĵ�ΪԲ�ģ������ζԽ��߳�Ϊ�뾶����Բ���������ڵ�A�͵�B�����A��ʾ�����ǣ�������
��ͼ��������ĵ�λ�����߶�Ϊ����һ�������Σ��Ա�ʾ��2�ĵ�ΪԲ�ģ������ζԽ��߳�Ϊ�뾶����Բ���������ڵ�A�͵�B�����A��ʾ�����ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\sqrt{2}$-1 | C�� | 2-$\sqrt{2}$ | D�� | $\sqrt{2}$-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
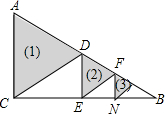 ��ͼ���ڡ�ABC�У���ACB=90�㣬��A=60�㣬AC=a����б��AB������CD���õ���1��������ACD��DE��BC�ڵ�E����Rt��BDEб��DB������EF���õ���2��������DEF����������ȥ�����1�������ε��������$\frac{\sqrt{3}}{4}$a2����n�������ε��������$\frac{\sqrt{3}{a}^{2}}{{2}^{2n}}$��
��ͼ���ڡ�ABC�У���ACB=90�㣬��A=60�㣬AC=a����б��AB������CD���õ���1��������ACD��DE��BC�ڵ�E����Rt��BDEб��DB������EF���õ���2��������DEF����������ȥ�����1�������ε��������$\frac{\sqrt{3}}{4}$a2����n�������ε��������$\frac{\sqrt{3}{a}^{2}}{{2}^{2n}}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��С����������1 | B�� | ����ֵ��С������0 | ||
| C�� | ���ĸ�������-1 | D�� | -2��ƽ������-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+y | B�� | x-y | C�� | -x-y | D�� | -x+y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com