
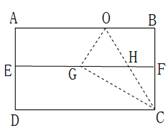
用尺规三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.如图所示,具体做法:(1)将一矩形纸片ABCD对折,EF为折痕;(2)继续沿过点C的直线CO对折,使点B落在EF上得到点G,则CO、CG就把∠BCD三等分了.请你写出它的推理过程.
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
| 1 | 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 “用直尺和圆规三等分任意角是世界三大几何作图不能问题之一”,2000多年来吸引了无数的数学爱好者为此探索和努力!
“用直尺和圆规三等分任意角是世界三大几何作图不能问题之一”,2000多年来吸引了无数的数学爱好者为此探索和努力!查看答案和解析>>
科目:初中数学 来源:2012届辽宁省鞍山市九年级第一次中考模拟考试数学试卷(带解析) 题型:解答题
用尺规三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.如图所示,具体做法:(1)将一矩形纸片ABCD对折,EF为折痕;(2)继续沿过点C的直线CO对折,使点B落在EF上得到点G,则CO、CG就把∠BCD三等分了.请你写出它的推理过程.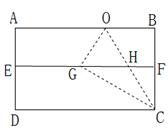
查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁省鞍山市九年级第一次中考模拟考试数学试卷(解析版) 题型:解答题
用尺规三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.如图所示,具体做法:(1)将一矩形纸片ABCD对折,EF为折痕;(2)继续沿过点C的直线CO对折,使点B落在EF上得到点G,则CO、CG就把∠BCD三等分了.请你写出它的推理过程.
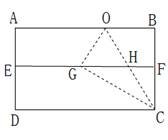
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com