
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: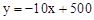 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
(1)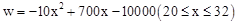 ;(2)当销售单价定为32元时,每月可获得最大利润,最大利润是2160元;(3)3600.
;(2)当销售单价定为32元时,每月可获得最大利润,最大利润是2160元;(3)3600.
【解析】
试题分析:(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价-进价)×销售量,从而列出关系式;
(2)首先确定二次函数的对称轴,然后根据其增减性确定最大利润即可;
(3)根据抛物线的性质和图象,求出每月的成本.
试题解析:(1)由题意,得:
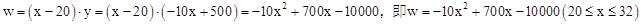 .
.
(2)函数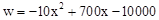 的图象的对称轴是直线
的图象的对称轴是直线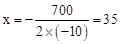 ,
,
又∵a=-10<0,抛物线开口向下.∴当20≤x≤32时,w随着x的增大而增大。
∴当x=32时,w=2160.
答:当销售单价定为32元时,每月可获得最大利润,最大利润是2160元.
(3)取w=2000得,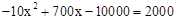 ,解这个方程得:x1=30,x2=40。
,解这个方程得:x1=30,x2=40。
∵a=-10<0,抛物线开口向下.
∴当30≤x≤40时,w≥2000.
∵20≤x≤32,∴当30≤x≤32时,w≥2000.
设每月的成本为P(元),由题意,得 ,
,
∵k=-200<0,∴P随x的增大而减小.
∴当x=32时,P的值最小,P最小值=3600.
答:想要每月获得的利润不低于2000元,小明每月的成本最少为3600元.
考点:一、二次函数和一元二次方程的应用.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届浙江省湖州市六校联考九年级上学期期末考试数学试卷(带解析) 题型:解答题
(本题10分)小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: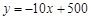 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省湖州市六校联考九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题10分)小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: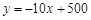 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com