
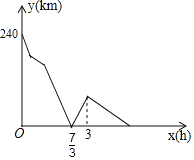
ЁОЬтФПЁПМзЁЂввСНГЕЗжБ№ДгЯрОр240ЧЇУзЕФAЃЌBСНЕиЭЌЪБЯрЯђдШЫйГіЗЂЃЌМзГЕГіЗЂ0.5аЁЪБКѓЗЂЯжгаЖЋЮїТфдкГіЗЂЕиAЕиЃЌгкЪЧСЂМДАДдЫйбидТЗЗЕЛиЃЌдкAЕиШЁЕНЖЋЮїКѓСЂМДвддЫйМЬајЯђBЕиааЪЛЃЌВЂдкЭОжагыввГЕЕквЛДЮЯргіЃЌЯргіКѓМзЁЂввСНГЕМЬајвдИїздЕФЫйЖШГЏзХИїздЕФЗНЯђдШЫйааЪЛЃЌЕБввГЕЕНДяAЕиКѓЃЌСЂМДЕєЭЗвддЫйПЊЭљBЕиЃЈМзГЕШЁЖЋЮїЁЂЕєЭЗКЭввГЕЕєЭЗЕФЪБМфОљКіТдВЛМЦЃЉЃЎСНГЕжЎМфЕФОрРыyЃЈЧЇУзЃЉгыМзГЕГіЗЂЕФЪБМфxЃЈаЁЪБЃЉжЎМфЕФВПЗжЙиЯЕШчЭМЫљЪОЃЌдђЕБввГЕЕНДяBЕиЪБЃЌМзГЕгыBЕиЕФОрРыЮЊ_____ЧЇУзЃЎ
ЁОД№АИЁП40
ЁОНтЮіЁП
гЩЭМЯѓПЩЕУ![]() аЁЪБЪБЃЌМзввСНГЕЯргіЃЌ3аЁЪБввГЕЕНДяAЕиЃЌПЩЧѓввЕФЫйЖШ240ЁТ3=80ЧЇУз/аЁЪБЃЌЫљвдМзЕФЫйЖШЃЈ240-80ЁС
аЁЪБЪБЃЌМзввСНГЕЯргіЃЌ3аЁЪБввГЕЕНДяAЕиЃЌПЩЧѓввЕФЫйЖШ240ЁТ3=80ЧЇУз/аЁЪБЃЌЫљвдМзЕФЫйЖШЃЈ240-80ЁС![]() ЃЉЁТЃЈ
ЃЉЁТЃЈ![]() 0.5ЁС2ЃЉ=40ЧЇУз/аЁЪБЃЌгЩввЗЕЛиBЕивВаш3аЁЪБЃЌМДввзмЙВЪБМфЮЊ6аЁЪБЃЌМДМзжиаТДгAГіЗЂЕНввЕНДяBЕиЫљгУЪБМфЮЊ6-0.5ЁС2=5аЁЪБЃЌМДПЩЧѓМзгыBЕиЕФОрРыЃЎ
0.5ЁС2ЃЉ=40ЧЇУз/аЁЪБЃЌгЩввЗЕЛиBЕивВаш3аЁЪБЃЌМДввзмЙВЪБМфЮЊ6аЁЪБЃЌМДМзжиаТДгAГіЗЂЕНввЕНДяBЕиЫљгУЪБМфЮЊ6-0.5ЁС2=5аЁЪБЃЌМДПЩЧѓМзгыBЕиЕФОрРыЃЎ
НтЃКгЩЭМЯѓПЩЕУ![]() аЁЪБЪБЃЌМзввСНГЕЯргіЃЌ3аЁЪБввГЕЕНДяAЕиЃЌ
аЁЪБЪБЃЌМзввСНГЕЯргіЃЌ3аЁЪБввГЕЕНДяAЕиЃЌ
ЁрввЕФЫйЖШ240ЁТ3ЃН80ЧЇУз/аЁЪБЃЌ
ЁрМзЕФЫйЖШЃЈ240Љ80ЁС![]() ЃЉЁТЃЈ
ЃЉЁТЃЈ![]() 0.5ЁС2ЃЉЃН40ЧЇУз/аЁЪБЃЌ
0.5ЁС2ЃЉЃН40ЧЇУз/аЁЪБЃЌ
ЁпввЗЕЛиBЕивВаш3аЁЪБЃЌ
ЁрМзгыBЕФОрРыЮЊ240Љ40ЃЈ6Љ0.5ЁС2ЃЉЃН40ЧЇУзЃЎ
ЙЪД№АИЮЊ40ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯ
ВФСЯ1ЃКЖдГЦЃЌвВаэЪЧжаЙњШЫзюЯВЛЖЕФЁЃНЈжўЪІСКЫМГЩдјЫЕЙ§ЃКЁАЮоТлЖЋЗНЁЂЮїЗНЃЌдйУЛгавЛИіУёзхЖджажсЖдГЦЯпШчДЫжгАЎгыуЁЪиЁЃЁБЗХблжаЙњЕФНЈжўЃЌЮоТлЪЧЙЌЕюЁЂУэгюЁЂЭЄЬЈЁЂТЅИѓЁЂдАСжЮоВЛгазХЖдГЦжЎУРЁЃЪ§бЇЪРНчвВРягавЛаЉе§ећЪ§ФуЮоТлДгзѓЭљгвПДЃЌЛЙЪЧДггвЭљзѓПДЃЌЪ§зжЖМЪЧЭъШЋвЛбљЕФЃЌР§ШчЃК11ЁЂ101ЁЂ2332ЁЂ1234321ЁЂЁЃЌЯёетбљЕФЪ§ЮвУЧНаЫќЁАЖдГЦЪ§ЁБЃЎ
ВФСЯ2ЃКШчЙћвЛИіШ§ЮЛЪ§![]() ЃЌТњзуa+b+cЃН8ЃЌЮвУЧОЭГЦетИіШ§ЮЛЪ§ЮЊЁАЗЂВЦЪ§ЁБЃЎ
ЃЌТњзуa+b+cЃН8ЃЌЮвУЧОЭГЦетИіШ§ЮЛЪ§ЮЊЁАЗЂВЦЪ§ЁБЃЎ
ЃЈ1ЃЉЧыжБНгаДГіМШЪЧЁАЖдГЦЪ§ЁБгжЪЧЁАЗЂВЦЪ§ЁБЕФЫљгаШ§ЮЛЪ§ЃЛ
ЃЈ2ЃЉвЛИіШ§ЮЛЁАЖдГЦЪ§ЁБЪЎЮЛЪ§зжЮЊ7ЃЌЫќЕФИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЪЧвЛИіздШЛЪ§ЕФЦНЗНЃЌЧѓетИіШ§ЮЛЪ§ЃЈЧыаДГіБивЊЕФЭЦРэЙ§ГЬЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
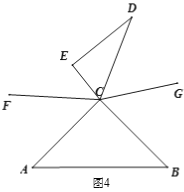
ЁОЬтФПЁПвбжЊНЋвЛИБШ§НЧАх(жБНЧШ§НЧАхABCКЭжБНЧШ§НЧАхCDEЃЌЁЯACBЃН90ЁуЃЌЁЯECDЃН60Ёу)ШчЭМ1АкЗХЃЌЕуDЁЂAЁЂCдквЛЬѕжБЯпЩЯЃЌНЋжБНЧШ§НЧАхCDEШЦЕуCФцЪБеыЗНЯђзЊЖЏЃЌБфЛЏАкЗХШчЭМЮЛжУ.
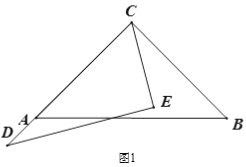
(1) ШчЭМ2ЃЌЕБЁЯACDЮЊЖрЩйЖШЪБЃЌCBЧЁКУЦНЗжЁЯECDЃП
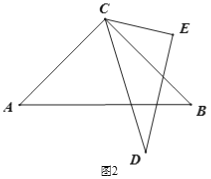
(2) ШчЭМ3ЃЌЕБШ§НЧАхCDEАкЗХдкЁЯACBФкВПЪБЃЌзїЩфЯпCFЦНЗжЁЯACEЃЌЩфЯпCGЦНЗжЁЯBCDЃЌШчЙћШ§НЧаЮCDEдкЁЯACBФкШЦЕуCШЮвтзЊЖЏЃЌЁЯFCGЕФЖШЪ§ЪЧЗёЗЂЩњБфЛЏЃПШчЙћВЛБфЃЌЧѓЦфжЕЃЛШчЙћБфЛЏЃЌЫЕУїРэгЩ.
(3) ШчЭМ4ЃЌЕБШ§НЧАхCDEзЊЕНЁЯACBЭтВПЪБЃЌЩфЯпCFЁЂCGШдШЛЗжБ№ЦНЗжЁЯACEЁЂЁЯBCDЃЌдка§зЊЙ§ГЬжаЃЌ(2)жаЕФНсТлЪЧЗёГЩСЂЃПШчЙћНсТлГЩСЂЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛГЩСЂЃЌЧыаДГіФуЕФНсТлВЂИљОнЭМ4ЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЬэМгЯТСаЬѕМўВЛФмЭЦЕУЫФБпаЮ
ЃЌЬэМгЯТСаЬѕМўВЛФмЭЦЕУЫФБпаЮ![]() ЮЊСтаЮЕФЪЧЃЈ ЃЉ
ЮЊСтаЮЕФЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЌBСНЕудкЪ§жсЩЯЖдгІЕФЪ§ЗжБ№ЮЊaЃЌbЃЌЧвЕуAдкЕуBЕФзѓБпЃЌ|a|=10ЃЌa+b=80ЃЌabЃМ0ЃЎ
ЃЈ1ЃЉЧѓГіaЃЌbЕФжЕЃЛ
ЃЈ2ЃЉЯжгавЛжЛЕчзгТьвЯPДгЕуAГіЗЂЃЌвд3ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШЯђгвдЫЖЏЃЌЭЌЪБСэвЛжЛЕчзгТьвЯQДгЕуBГіЗЂЃЌвд2ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШЯђзѓдЫЖЏЃЎ
ЂйЩшСНжЛЕчзгТьвЯдкЪ§жсЩЯЕФЕуCЯргіЃЌЧѓГіЕуCЖдгІЕФЪ§ЪЧЖрЩйЃП
ЂкОЙ§ЖрГЄЪБМфСНжЛЕчзгТьвЯдкЪ§жсЩЯЯрОр20ИіЕЅЮЛГЄЖШЃП
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП[аТЖЈвх]: ![]() ЮЊЪ§жсЩЯШ§ЕуЃЌШєЕу
ЮЊЪ§жсЩЯШ§ЕуЃЌШєЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыЪЧЕу
ЕФОрРыЪЧЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыЕФ3БЖЃЌЮвУЧОЭГЦЕу
ЕФОрРыЕФ3БЖЃЌЮвУЧОЭГЦЕу![]() ЕФавдЫЕу.
ЕФавдЫЕу.
[ЬиР§ИажЊ]
ЃЈ1ЃЉШчЭМ1ЃЌЕу![]() БэЪОЕФЪ§ЮЊ-1ЃЌЕу
БэЪОЕФЪ§ЮЊ-1ЃЌЕу![]() БэЪОЕФЪ§ЮЊ3.БэЪО2ЕФЕу
БэЪОЕФЪ§ЮЊ3.БэЪО2ЕФЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыЪЧ3ЃЌЕНЕу
ЕФОрРыЪЧ3ЃЌЕНЕу![]() ЕФОрРыЪЧ1ЃЌФЧУДЕу
ЕФОрРыЪЧ1ЃЌФЧУДЕу![]() ЪЧ
ЪЧ![]() ЕФавдЫЕуЃЌ
ЕФавдЫЕуЃЌ
Ђй![]() ЕФавдЫЕуБэЪОЕФЪ§ЪЧ________ЃЛ
ЕФавдЫЕуБэЪОЕФЪ§ЪЧ________ЃЛ
A.-1 B.0 C.1 D.2
ЂкЪдЫЕУї![]() ЕФавдЫЕу.
ЕФавдЫЕу.
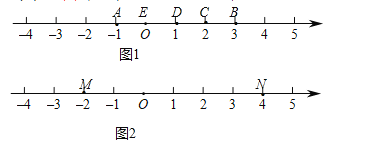
ЃЈ2ЃЉШчЭМ2ЃЌ ![]() ЮЊЪ§жсЩЯСНЕуЃЌЕу
ЮЊЪ§жсЩЯСНЕуЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ-2ЃЌЕу
ЫљБэЪОЕФЪ§ЮЊ-2ЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ4ЃЌ
ЫљБэЪОЕФЪ§ЮЊ4ЃЌ
дђ![]() ЕФавдЫЕуБэЪОЕФЪ§ЮЊ________.
ЕФавдЫЕуБэЪОЕФЪ§ЮЊ________.
[ЭиеЙгІгУ]
ЃЈ3ЃЉШчЭМ3ЃЌ ![]() ЮЊЪ§жсЩЯСНЕуЃЌЕу
ЮЊЪ§жсЩЯСНЕуЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ-20ЃЌЕу
ЫљБэЪОЕФЪ§ЮЊ-20ЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ40.гавЛжЛЕчзгТьвЯ
ЫљБэЪОЕФЪ§ЮЊ40.гавЛжЛЕчзгТьвЯ![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвд5ИіЕЅЮЛУПУыЕФЫйЖШЯђзѓдЫЖЏЃЌЕНДяЕу
ГіЗЂЃЌвд5ИіЕЅЮЛУПУыЕФЫйЖШЯђзѓдЫЖЏЃЌЕНДяЕу![]() ЭЃжЙ.ЕБtЮЊКЮжЕЪБЃЌ
ЭЃжЙ.ЕБtЮЊКЮжЕЪБЃЌ![]() ЁЂ
ЁЂ![]() КЭ
КЭ![]() Ш§ИіЕужаЧЁКУгавЛИіЕуЮЊЦфгрСНЕуЕФавдЫЕу?
Ш§ИіЕужаЧЁКУгавЛИіЕуЮЊЦфгрСНЕуЕФавдЫЕу?

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
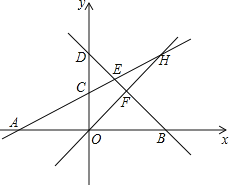
ЁОЬтФПЁПШчЭМЃЌжБЯпACЃКyЃН![]() x+2ЗжБ№НЛxжсКЭyжсгкAЃЌCСНЕуЃЌжБЯпBDЃКyЃНЉx+bЗжБ№НЛxжсКЭyжсгкBЃЌDСНЕуЃЌжБЯпACгыBDНЛгкЕуEЃЌЧвOAЃНOBЃЎ
x+2ЗжБ№НЛxжсКЭyжсгкAЃЌCСНЕуЃЌжБЯпBDЃКyЃНЉx+bЗжБ№НЛxжсКЭyжсгкBЃЌDСНЕуЃЌжБЯпACгыBDНЛгкЕуEЃЌЧвOAЃНOBЃЎ
ЃЈ1ЃЉЧѓжБЯпBDЕФНтЮіЪНКЭEЕФзјБъЃЎ
ЃЈ2ЃЉШєжБЯпyЃНxЗжБ№гыжБЯпACЃЌBDНЛгкЕуHКЭFЃЌЧѓЫФБпаЮECOFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌAЁЂBЮЊxжсЩЯСНЕуЃЌCЁЂDЮЊyжсЩЯЕФСНЕуЃЌОЙ§ЕуAЁЂCЁЂBЕФХзЮяЯпЕФвЛВПЗжc1гыОЙ§ЕуAЁЂDЁЂBЕФХзЮяЯпЕФвЛВПЗжc2зщКЯГЩвЛЬѕЗтБеЧњЯпЃЌЮвУЧАбетЬѕЗтБеЧњЯпГЩЮЊЁАЕАЯпЁБЃЎвбжЊЕуCЕФзјБъЮЊЃЈ0ЃЌЉ![]() ЃЉЃЌЕуMЪЧХзЮяЯпC2ЃКy=mx2Љ2mxЉ3mЃЈmЃМ0ЃЉЕФЖЅЕуЃЎ
ЃЉЃЌЕуMЪЧХзЮяЯпC2ЃКy=mx2Љ2mxЉ3mЃЈmЃМ0ЃЉЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЁАЕАЯпЁБдкЕкЫФЯѓЯоЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУЁїPBCЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЁїPBCУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЁїBDMЮЊжБНЧШ§НЧаЮЪБЃЌЧѓmЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЌЪБХзжРAЃЌBСНИіОљдШЕФаЁСЂЗНЬх(УПИіУцЩЯЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6)ЃЌЩшСНСЂЗНЬхГЏЩЯЕФЪ§зжЗжБ№ЮЊxЃЌyЃЌВЂвдДЫШЗЖЈЕуP(xЃЌy)ЃЌФЧУДЕуPТфдкжБЯпyЃНЃ2xЃЋ9ЩЯЕФИХТЪЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com