
如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.

(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
(1)由1(cm/s)
(2)FG段的函数表达式为: (6≤t≤9)。
(6≤t≤9)。
(3)存在。理由见解析。
解析分析:(1)根据函数图象中E点所代表的实际意义求解.E点表示点P运动到与点B重合时的情形,运动时间为3s,可得AB=6cm;再由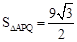 ,可求得AQ的长度,进而得到点Q的运动速度。
,可求得AQ的长度,进而得到点Q的运动速度。
(2)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.如答图2所示,求出S的表达式,并确定t的取值范围。
(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示,求出t的值。当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示,求出t的值。
解:(1)由题意,可知题图2中点E表示点P运动至点B时的情形,所用时间为3s,则菱形的边长AB=2×3=6cm。
此时如图1所示,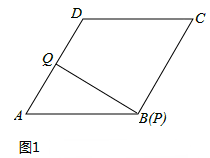
AQ边上的高 ,
, ,解得AQ=3(cm)。
,解得AQ=3(cm)。
∴点Q的运动速度为:3÷3=1(cm/s)。
(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形,如图2所示,
点Q运动至点D所需时间为:6÷1=6s,点P运动至点C所需时间为12÷2=6s,至终点D所需时间为18÷2=9s。
因此在FG段内,点Q运动至点D停止运动,点P在线段CD上继续运动,且时间t的取值范围为:6≤t≤9。
过点P作PE⊥AD交AD的延长线于点E,则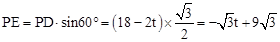
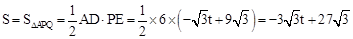 。
。
∴FG段的函数表达式为: (6≤t≤9)。
(6≤t≤9)。
(3)存在。
菱形ABCD的面积为:6×6×sin60°=18 。
。
当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如图3所示,
此时△APQ的面积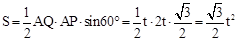 。
。
根据题意,得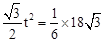 ,解得
,解得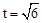 s。
s。
当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如图4所示,
此时,有 ,
,
即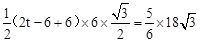 ,解得
,解得 s。
s。
综上所述,存在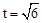 s和t=
s和t= s,使PQ将菱形ABCD的面积恰好分成1:5的两部分。
s,使PQ将菱形ABCD的面积恰好分成1:5的两部分。


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
(1)在图1中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),请写出图中的顶点C的坐标( _________ , _________ ).
(2)在图2中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),求出图中的标点C的坐标,并说明理由(C点坐标用含c,d,e的代数式表示).
归纳与发现
(3)通过对图1,2的观察,你会发现:图3中的平行四边形ABCD的顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,则横坐标a,c,m,e之间的等量关系为 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )




A B C D
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
A. &nbs, &nbs, | B. &nbs, &nbs, | C. &nbs, &nbs, | D. &nbs, &nbs, |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
有两块面积相同的小麦试验田,分别收获小麦9000kg和15000kg.已知第一块试验田每公顷的产量比第二块少3000kg,若设第一块试验田每公顷的产量为xkg,根据题意,可得方程 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com