
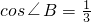 ,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点
,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点 E作EF⊥BC交AC边于点F.
E作EF⊥BC交AC边于点F. 解:(1)过点A作AM⊥BC,垂足为点M,
解:(1)过点A作AM⊥BC,垂足为点M, ,AB=3,
,AB=3, ,
, -6
-6 x.
x. -6
-6 x.
x. -
- .
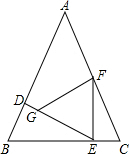
.
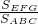 =(
=( )2
)2 =(
=(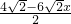 )2
)2 x2-48
x2-48 x+16
x+16 .
. -6
-6 x)=3:GE,
x)=3:GE, -9
-9 x.
x. x.
x. x-(6
x-(6 -9
-9 x)=11
x)=11 x-6
x-6 .
. x-6
x-6 ≥0,且6
≥0,且6 -9
-9 x>0,
x>0,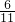 ≤x<
≤x< .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |
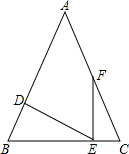 E作EF⊥BC交AC边于点F.
E作EF⊥BC交AC边于点F.查看答案和解析>>
科目:初中数学 来源:2010年上海市静安区初三数学中考模拟试卷(12月份)(解析版) 题型:解答题
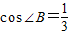 ,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.
,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.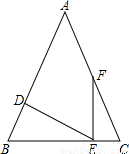
查看答案和解析>>
科目:初中数学 来源:2009年上海市卢湾区中考数学二模试卷(解析版) 题型:解答题
 ,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.
,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com