
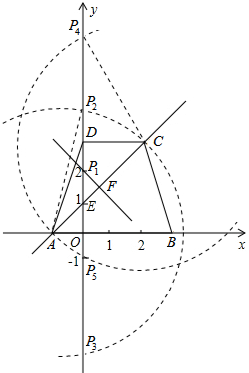
 (2013•云南)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC与y轴交于点E(0,1),点C的坐标为(2,3).
(2013•云南)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC与y轴交于点E(0,1),点C的坐标为(2,3).
|
|
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
| AP22-OA2 |
(3
|
| 17 |
| 17 |
| 17 |
| 2 |
| 2 |
| CP42-CD2 |
(3
|
| 14 |
| 14 |
| 14 |
| 14 |
| 17 |
| 17 |
| 14 |
| 14 |


科目:初中数学 来源: 题型:
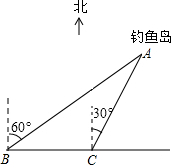 (2013•云南)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
(2013•云南)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?查看答案和解析>>
科目:初中数学 来源: 题型:
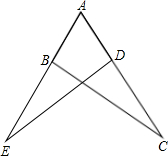 (2013•云南)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).
(2013•云南)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•云南)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(2013•云南)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•云南)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.
(2013•云南)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com