
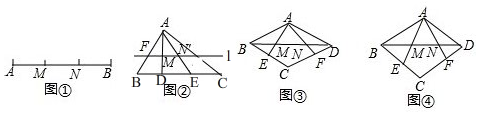
分析 (1)分两种情况进行讨论:NB为最长线段;MN为最长线段,分别根据勾股定理进行计算即可;
(2)根据BD=3,DE=5,EC=4,可得DE2=BD2+EC2,再根据直线l∥BC,可得$\frac{AF}{AB}$=$\frac{AM}{AD}$$\frac{AN}{AE}$,故可设$\frac{FM}{BD}$=$\frac{MN}{DE}$=$\frac{NG}{EC}$=k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2,可得MN2=FM2+NG2,即点M,N是线段FG的勾股分割点;
(3)①先判定△BEM∽△DAM,得出$\frac{BM}{DM}$=$\frac{BE}{DA}$,再根据BE=$\frac{1}{2}$BC,可得出BM=$\frac{1}{2}$DM,BM=$\frac{1}{3}$BD,同理可得,DN=$\frac{1}{4}$BD,进而得到MN=BD-BM-DN=$\frac{5}{12}$BD,再根据MN2=BM2+ND2,可得M、N是线段BD的勾股分割点.
②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM=$\frac{12}{13}$,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
解答 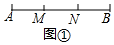 解:(1)当NB为最长线段时,
解:(1)当NB为最长线段时,
∵M、N是线段AB的勾股分割点,AM=6,MN=8,
∴NB=$\sqrt{A{M}^{2}+M{N}^{2}}$=10;
当MN为最长线段时,
NB=$\sqrt{M{N}^{2}-A{M}^{2}}$=2$\sqrt{7}$,
综上所述,NB的值为10或2$\sqrt{7}$;
(2)证明:如图2,∵BD=3,DE=5,EC=4,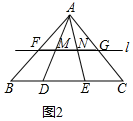
∴DE2=BD2+EC2,
∵直线l∥BC,
∴$\frac{AF}{AB}$=$\frac{AM}{AD}$$\frac{AN}{AE}$,
∴可设$\frac{FM}{BD}$=$\frac{MN}{DE}$=$\frac{NG}{EC}$=k,
∴FM=kBD,MN=kDE,NG=kEC,
∵DE2=BD2+EC2,
∴MN2=FM2+NG2,
∴点M,N是线段FG的勾股分割点;
(3)①证明:如图3,∵四边形ABCD是菱形,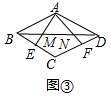
∴AD∥BE,AB=BC=CD=DA,
∴△BEM∽△DAM,
∴$\frac{BM}{DM}$=$\frac{BE}{DA}$,
∵BE=$\frac{1}{2}$BC,
∴BM=$\frac{1}{2}$DM,BM=$\frac{1}{3}$BD,
同理可得,DN=$\frac{1}{4}$BD,
∴MN=BD-BM-DN=$\frac{5}{12}$BD,
∵MN2=$\frac{25}{144}$BD2,BM2+ND2=$\frac{1}{9}$BD2+$\frac{1}{16}$BD2=$\frac{25}{144}$BD2,
∴MN2=BM2+ND2,
∴M、N是线段BD的勾股分割点.
②如图4,将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,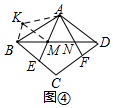
∴∠KBM=∠KBA+∠ABM=∠ABC,
∵sinβ=$\frac{12}{13}$,
∴sin∠KBM=$\frac{12}{13}$,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠KAM=∠NAM,
∵AN=AK,AM=AM,
∴△KAM≌△NAM,
∴KM=NM,
∵点M、N是线段BD的勾股分割点,
∴△KBM是直角三角形,
∵sin∠KBM=$\frac{12}{13}$,
∴BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
点评 本题属于四边形综合题,主要考查了勾股定理的逆定理,菱形的性质,相似三角形的判定与性质以及全等三角形的判定与性质的综合应用,解决问题的关键是掌握:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.解题时注意辅助线的运用以及旋转变换的运用,构造全等三角形以及直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
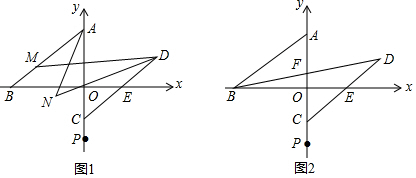
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
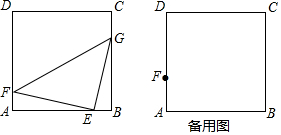
 如图,在Rt△ABC中,∠ABC=90°,∠ACB=60°,将Rt△ABC绕点C逆时针旋转60°得到△DGC,点G在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABE,连接AD.
如图,在Rt△ABC中,∠ABC=90°,∠ACB=60°,将Rt△ABC绕点C逆时针旋转60°得到△DGC,点G在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABE,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
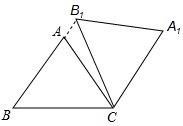 在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA延长线上(如图).
在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA延长线上(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
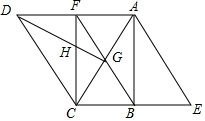
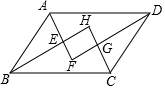 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
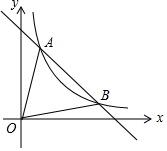 如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com