
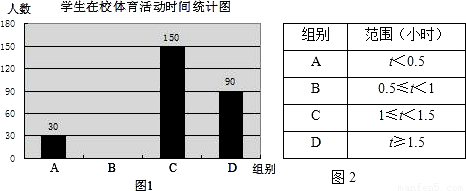
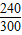 =0.8,则64000名中小学达到国家规定体育活动时间(不低于1小时)的人数约有0.8×64000=51200人.
=0.8,则64000名中小学达到国家规定体育活动时间(不低于1小时)的人数约有0.8×64000=51200人.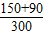 ×64000=51200人.
×64000=51200人.

科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
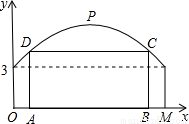
查看答案和解析>>
科目:初中数学 来源:2010年河南省中考数学模拟试卷(11)(解析版) 题型:解答题
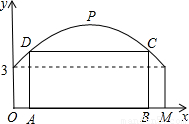
查看答案和解析>>
科目:初中数学 来源:2009年河北省唐山市中考数学一模试卷(解析版) 题型:解答题
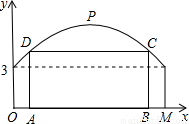
查看答案和解析>>
科目:初中数学 来源:2009年广东省揭阳市普宁市燎原中学中考数学二模试卷(解析版) 题型:解答题
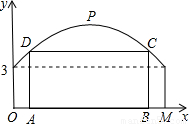
查看答案和解析>>
科目:初中数学 来源:2008年广东省佛山市中考数学试卷(解析版) 题型:解答题
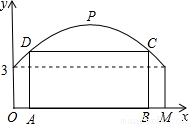
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com