
平面内的两条直线有相交和平行两种位置关系.
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
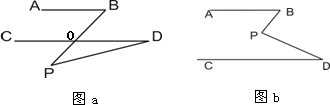
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明);
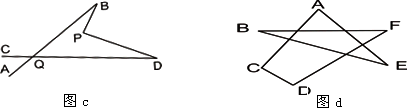
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com