解:(1)∵(x+

)
2=x
2+2+

=9,
∴x
2+

=7,
∴x
4+

=(x
2+

)
2-2=49-2=47;
(2)原式=(4x
2+4xy+y
2-y
2-4xy-8x)÷2x
=(4x2-8x)÷2x
=2x-4,
当x=2时,原式=2×2-4=0.
分析:(1)在x+

=3的基础上,左右平方,易求x
2+

的值,再在x
2+

=7的基础上左右平方可求x
4+

的值;
(2)先根据完全平方公式、单项式乘以多项式的法则计算,再合并,最后根据多项式除以单项式的法则计算出结果,然后把x的值代入计算即可.
点评:本题考查了整式的化简求值,解题的关键是公式的使用、以及去括号、合并同类项.

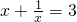 ,求
,求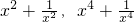 的值.
的值.