
分析 (1)根据判别式的意义得到△=(2k)2-4(k2-2k+1)=8k-4≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=-2k,x1x2=k2-2k+1,再利用完全平方公式由x12+x22=4得到(x1+x2)2-2x1x2=4,则4k2-2(k2-2k+1)=4,然后解关于k的方程,最后利用k的范围可确定满足条件的k的值.
解答 解:(1)根据题意得△=(2k)2-4(k2-2k+1)=8k-4≥0,
解得k≥$\frac{1}{2}$;
(2)根据题意得x1+x2=-2k,x1x2=k2-2k+1,
∵x12+x22=4,
∴(x1+x2)2-2x1x2=4
∴4k2-2(k2-2k+1)=4,
整理得k2+2k-3=0,解得k1=-3,k2=1,
而k≥$\frac{1}{2}$
∴k=1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
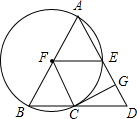 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
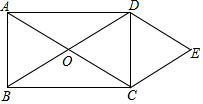 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com