
如图,已知动点A在函数y= (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴、y轴于点P,Q.当QE∶DP=4∶9时,图中阴影部分的面积等于 .
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴、y轴于点P,Q.当QE∶DP=4∶9时,图中阴影部分的面积等于 .
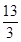 .
.
解析试题分析:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t,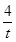 ),则AD=AB=DG=
),则AD=AB=DG=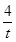 ,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=
,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=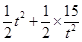 ,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=
,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=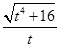 ,再由△EFQ∽△DAE,求出
,再由△EFQ∽△DAE,求出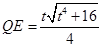 ,△ADE∽△GPD,求出DP=
,△ADE∽△GPD,求出DP=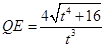 ,然后根据QE:DP=4:9,即可得出t2=
,然后根据QE:DP=4:9,即可得出t2=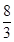 .
.
试题解析:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t,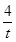 ),则AD=AB=DG=
),则AD=AB=DG=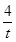 ,AE=AC=EF=t.
,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得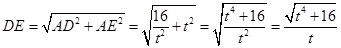 .
.
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴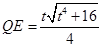 ,
,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴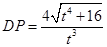 .
.
又∵QE:DP=4:9,
∴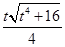 :
: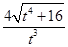 =4:9,
=4:9,
解得t2=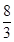 .
.
∴图中阴影部分的面积=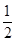 AC2+
AC2+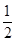 AB2=
AB2=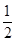 t2+
t2+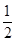 ×
×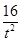 =
=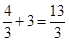 .
.
考点: 反比例函数综合题.


科目:初中数学 来源: 题型:填空题
如图,反比例函数y= (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,点P在双曲线 (x>0)上,以P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF-OE=6,则k的值是 .
(x>0)上,以P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF-OE=6,则k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
反比例函数y1= ,y2=
,y2= (k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= _________ .
(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,在平面直角坐标系中,ΔABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数 的图象上.反比例函数
的图象上.反比例函数 的图象经过点C,交AB于点D,则点D的坐标是 .
的图象经过点C,交AB于点D,则点D的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,Rt△ABC中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数 (x>0)的图象上运动,那么点B在函数 (填函数解析式)的图象上运动.
(x>0)的图象上运动,那么点B在函数 (填函数解析式)的图象上运动.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com