

解:(1)S阴影=2× ×4×5=20,S矩形ABCD=5×8=40;
×4×5=20,S矩形ABCD=5×8=40;
(2)S阴影=4×4÷2+4×5÷2=18,S梯形ABCD=(4+5)×8÷2=36;
(3)作CE⊥AB,交AB于E.
∵BC=AD=5,∠B=60°,
∴AE=sin60°×BC= .
.
S阴影= ×8×
×8× =10
=10 ,S四边形ABCD=8×
,S四边形ABCD=8× =20
=20 .
.
解决问题方案:连接CM,DM,则S△CMD= S□ABCD.把△CMD分给一家,其他部分分给另外一家即可.
S□ABCD.把△CMD分给一家,其他部分分给另外一家即可.
理由:
过M作ME⊥EB于E延长EM交DA于F.
∵AD∥BC,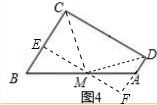
∴MF⊥AD,∠B=∠1.
又∵M为BA中点,
∴BM=MA.
∴△BEM≌△AFM.
∴EM=MF= EF.
EF.
S△CBM+S△DAM= BC•EM+
BC•EM+ AD•MF
AD•MF
= BC×
BC× EF+
EF+ AD×
AD× EF
EF
=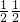 (BC+AD)•EF=
(BC+AD)•EF= S?ABCD.
S?ABCD.
∴S△CMD= S?ABCD.
S?ABCD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

| A、22.5° | B、67.5° | C、22.5°或67.5° | D、45°或135° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线y=
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com