
两条平行直线上各有 个点,用这
个点,用这 对点按如下的规则连结线段:①平行线之间的点连结线段时,可以有共同的端点,但不能有其他交点;②符合①要求的线段必须全部画出。图①展示了当
对点按如下的规则连结线段:①平行线之间的点连结线段时,可以有共同的端点,但不能有其他交点;②符合①要求的线段必须全部画出。图①展示了当 时的情况,此时图中三角形的个数为0;图②展示
时的情况,此时图中三角形的个数为0;图②展示 时的一种情况,此时图中三角形的个数为2.
时的一种情况,此时图中三角形的个数为2.
(1)当 时,请在图③中画出使三角形个数最少的图形,此时图中三角形的个数为 个。
时,请在图③中画出使三角形个数最少的图形,此时图中三角形的个数为 个。
(2)试猜想:当有 对点时,按上述规则画出的图形中,最少有多少个三角形?
对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当 时,按上述规则画出的图形中,最少有多少个三角形?
时,按上述规则画出的图形中,最少有多少个三角形?
(1)4个,如图所示;(2) 个;(3)4024个
个;(3)4024个

解析试题分析:(1)仔细分析题意,准确画出图形即可得到结果;
(2)分析可得,当 时图中三角形的个数为0,即
时图中三角形的个数为0,即 ;当
;当 时图中三角形的个数为2,即
时图中三角形的个数为2,即 ;…;根据这个规律即可得到当有n对点时,最少可以画的三角形的数目;
;…;根据这个规律即可得到当有n对点时,最少可以画的三角形的数目;
(3)把 代入(2)中得到的规律即可得到结果.
代入(2)中得到的规律即可得到结果.
(1)当 时,如图所示,此时图中三角形的个数为 4 个;
时,如图所示,此时图中三角形的个数为 4 个; 

(2)当 时图中三角形的个数为0,即
时图中三角形的个数为0,即 ;
;
当 时图中三角形的个数为2,即
时图中三角形的个数为2,即 ;
;
…;
则当有 对点时,按上述规则画出的图形中,最少有
对点时,按上述规则画出的图形中,最少有 个三角形;
个三角形;
(3)当 时,
时, (个),
(个),
答:当 时,按上述规则画出的图形中,最少有4024个三角形.
时,按上述规则画出的图形中,最少有4024个三角形.
考点:本题考查的是找规律-图形的变化
点评:解答本题的关键是要求学生通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题.


科目:初中数学 来源: 题型:
两条平行直线上各有![]() 个点,用这
个点,用这![]() 对点按如下的规则连接线段;
对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当![]() 时的情况,此时图中三角形的个数为0;
时的情况,此时图中三角形的个数为0;
图2展示了当![]() 时的一种情况,此时图中三角形的个数为2;
时的一种情况,此时图中三角形的个数为2;
(1)当![]() 时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形;
时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形;
(2)试猜想当![]() 对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能
对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能![]() 为多少?
为多少?

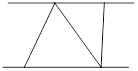

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
两条平行直线上各有个点,用这
对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当时的情况,此时图中三角形的个数为0;
图2展示了当时的一种情况,此时图中三角形的个数为2;
(1)当时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形;
(2)试猜想当对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能
为多少?
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
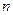 个点,用这
个点,用这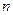 对点按如下的规则连接线段;
对点按如下的规则连接线段;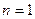 时的情况,此时图中三角形的个数为0;
时的情况,此时图中三角形的个数为0;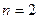 时的一种情况,此时图中三角形的个数为2;
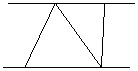
时的一种情况,此时图中三角形的个数为2;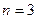 时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形;
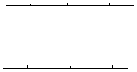
时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形; 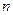 对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能
对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能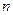 为多少?
为多少? 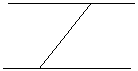
查看答案和解析>>
科目:初中数学 来源:2012-2013年浙江杭州萧山七年级12月月考数学试卷(解析版) 题型:解答题
两条平行直线上各有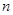 个点,用这
个点,用这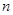 对点按如下的规则连结线段:①平行线之间的点连结线段时,可以有共同的端点,但不能有其他交点;②符合①要求的线段必须全部画出。图①展示了当
对点按如下的规则连结线段:①平行线之间的点连结线段时,可以有共同的端点,但不能有其他交点;②符合①要求的线段必须全部画出。图①展示了当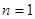 时的情况,此时图中三角形的个数为0;图②展示
时的情况,此时图中三角形的个数为0;图②展示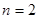 时的一种情况,此时图中三角形的个数为2.
时的一种情况,此时图中三角形的个数为2.
(1)当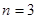 时,请在图③中画出使三角形个数最少的图形,此时图中三角形的个数为 个。
时,请在图③中画出使三角形个数最少的图形,此时图中三角形的个数为 个。
(2)试猜想:当有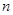 对点时,按上述规则画出的图形中,最少有多少个三角形?
对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当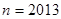 时,按上述规则画出的图形中,最少有多少个三角形?
时,按上述规则画出的图形中,最少有多少个三角形?

查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市卢湾区初三上学期期末第一次模拟数学卷 题型:解答题
两条平行直线上各有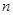 个点,用这
个点,用这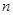 对点按如下的规则连接线段;
对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当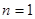 时的情况,此时图中三角形的个数为0;
时的情况,此时图中三角形的个数为0;
图2展示了当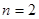 时的一种情况,此时图中三角形的个数为2;
时的一种情况,此时图中三角形的个数为2;
(1)当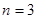 时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形;
时,请在图3中画出使三角形个数最少的图形,此时图中有 个三角形;
(2)试猜想当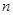 对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能
对点时,按上述规则画出的图形中,最少有多少个三角形?此时最少三角形的个数能否为2010个?如果能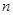 为多少?
为多少?



图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com