解:(1)设每个颜料盒为x元,每支水笔为y元,
根据题意得,
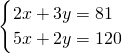
,
解得
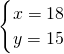
.
答:每个颜料盒为18元,每支水笔为15元;
(2)由题意知,y
1关于m的函数关系式是y
1=18×70%m,
即y
1=12.6m;
由题意知,买笔10支以下(含10支)没有优惠,
所以此时的函数关系式为:y
2=15m;
当买10支以上时,超出部分有优惠,
所以此时的函数关系式为:y
2=15×10+15×(m-10)×80%,
即y
2=30+12m;
(3)当y
1=y
2时,即12m+30=12.6m时,解得m=50,
当y
1>y
2时,即12.6m>12m+30时,解得m>50,
当y
1<y
2时,即12.6m<12m+30时,解得m<50,
综上所述,当购买奖品超过10件但少于50件时,买彩笔盒合算.
当购买奖品等于50件时,买水笔和彩笔盒钱数相同.
当购买奖品超过50件时,买水笔合算.
分析:(1)设每个颜料盒为x元,每支水笔为y元,然后列出方程组求解即可;
(2)根据颜料盒七折优惠表示出y
1与x的关系式;分0<x≤10和x>10两种情况,根据水笔八折优惠列式表示出y
2与x的关系式即可;
(3)分三种情况列式求出购买奖品件数,然后写出购买方法即可.
点评:本题考查了一次函数的应用,二元一次方程组的应用,比较简单,读懂题目信息,理清优惠的方法是解题的关键,(3)分情况列出不等式是解题的关键.

 某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒做为奖品.请你根据图中所给的信息,解答下列问题:
某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒做为奖品.请你根据图中所给的信息,解答下列问题: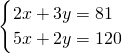 ,
,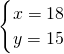 .
.

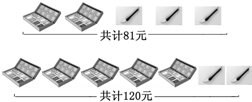 (2013•鄂尔多斯)某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒做为奖品.请你根据图中所给的信息,解答下列问题:
(2013•鄂尔多斯)某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒做为奖品.请你根据图中所给的信息,解答下列问题: