
分析 (1)因式分解法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)∵(x+2)(x-4)=0,
∴x+2=0或x-4=0,
解得:x=-2或x=4;
(2)解不等式x-3(x-1)<1,得:x>$\frac{5}{2}$,
解不等式$\frac{x-1}{2}$<1,得:x<3,
∴不等式组的解集为$\frac{5}{2}$<x<3.
点评 本题主要考查解一元二次方程和一元一次不等式组的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.


科目:初中数学 来源: 题型:解答题
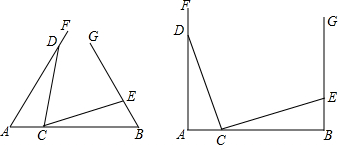
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
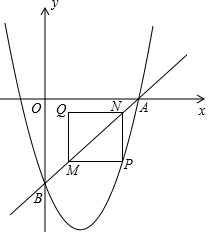 如图,直线y=2x-6与抛物线y=2x2+bx+c相交于A,B两点,点A在x轴上,点B在y轴上,点P在直线AB下方的抛物线上,过P点分别作PM∥x轴交AB于M点,PN∥y轴交AB于N点,以PM、PN为边作矩形PMQN,设点Q的坐标为(m,n).
如图,直线y=2x-6与抛物线y=2x2+bx+c相交于A,B两点,点A在x轴上,点B在y轴上,点P在直线AB下方的抛物线上,过P点分别作PM∥x轴交AB于M点,PN∥y轴交AB于N点,以PM、PN为边作矩形PMQN,设点Q的坐标为(m,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
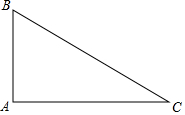 如图,已知在△ABC中,∠A=90°,请用尺规作⊙P,使圆心P在AC上,且与AB、BC两边都相切.(要求保留作图痕迹,不必写出作法和证明)
如图,已知在△ABC中,∠A=90°,请用尺规作⊙P,使圆心P在AC上,且与AB、BC两边都相切.(要求保留作图痕迹,不必写出作法和证明)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
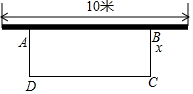 如图,某中学准备用铁栅栏围建一个长方形的花圃ABCD,且使花圃的面积为40平方米,其中靠墙的边为AB,已知墙的长度为10米,设BC的长为x米,DC的长为y米
如图,某中学准备用铁栅栏围建一个长方形的花圃ABCD,且使花圃的面积为40平方米,其中靠墙的边为AB,已知墙的长度为10米,设BC的长为x米,DC的长为y米查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com