Question

已知关于x、y的方程组的解都为正数．
（1）求m的取值范围；
（2）化简：|3m+2|-|m-5|．

Answer 1

解：（1），
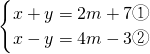
①+②得，2x=6m+4，
解得x=3m+2，
①-②得，2y=-2m+10，
解得y=-m+5，
∵x、y都是正数，
∴，
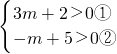
由①得，m＞-，
由②得，m＜5，
∴m的取值范围是-＜m＜5；

（2）根据（1）-＜m＜5，
所以，|3m+2|-|m-5|=3m+2+m-5=4m-3．
分析：（1）利用加减消元法解关于x、y的二元一次方程，用m表示出x、y，再根据方程组的解都是正数列出不等式组，然后解不等式组即可；
（2）根据m的取值范围去掉绝对值号合并同类项即可．
点评：本题考查了解一元一次不等式组，解二元一次方程组，把方程组中的字母m看作常数求出x、y的表达式是解题的关键．