
分析 过点O作OE⊥AB于E,交CD于F,连接OA、OC,如图,利用平行线的性质得OF⊥CD,则根据垂径定理得到AE=BE=$\frac{1}{2}$AB=6,CF=DF=$\frac{1}{2}$CD=8,再利用勾股定理计算出OE=8,OF=6,然后分类讨论:当点O在AB和CD之间时,EF=OE+OF=14,当点O不在AB和CD之间时,EF=OE-OF=2.
解答 解: 过点O作OE⊥AB于E,交CD于F,连接OA、OC,如图,
过点O作OE⊥AB于E,交CD于F,连接OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=$\frac{1}{2}$AB=6,CF=DF=$\frac{1}{2}$CD=8,
在Rt△AOE中,OE=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
在Rt△OCF中,OF=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
当点O在AB和CD之间时,EF=OE+OF=8+6=14,
当点O不在AB和CD之间时,EF=OE-OF=8-6=2,
∴AB、CD之间的距离为2或14.
故答案为2或14.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.注意分类讨论思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
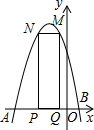 如图,二次函数y=-x2-2x+3的图象交x轴于A、B两点,交y轴于C点,矩形MNPQ的点M在抛物线上,边PQ在x轴上,则当点Q的坐标为多少时,矩形MNPQ的周长最大?
如图,二次函数y=-x2-2x+3的图象交x轴于A、B两点,交y轴于C点,矩形MNPQ的点M在抛物线上,边PQ在x轴上,则当点Q的坐标为多少时,矩形MNPQ的周长最大?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,等边三角形ABC的边长为4,点P为BC边上一点,且BP=1,点D为AC边上一点.若∠APD=60°,则CD的长为( )
如图,等边三角形ABC的边长为4,点P为BC边上一点,且BP=1,点D为AC边上一点.若∠APD=60°,则CD的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
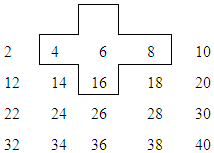 探索规律:将连续的偶数2,4,6,8,…,排成如表:
探索规律:将连续的偶数2,4,6,8,…,排成如表:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com