
 ��2013•�����ض�ģ����ͼ��������ABCO�ı�OA��OC���������ϣ���B���꣨3��3������������ABCO�Ƶ�A˳ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������ADEF��ED���߶�OC�ڵ�G��ED���ӳ��߽��߶�BC�ڵ�P����AP��AG��
��2013•�����ض�ģ����ͼ��������ABCO�ı�OA��OC���������ϣ���B���꣨3��3������������ABCO�Ƶ�A˳ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������ADEF��ED���߶�OC�ڵ�G��ED���ӳ��߽��߶�BC�ڵ�P����AP��AG��
|
| 3 |
| 3 |
| 3 |
| CG |
| tan30�� |
3-
| ||||
|
| 3 |
| 3 |
|
|
| 3 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
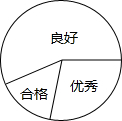 ��2013•�����ض�ģ�����꼶��3������ĩ���Ժϸ����á�����ı�����1��6��3��С��ͬѧ����һ���뾶Ϊ2cm��Բ�ε�ͳ��ͼ����ͼ�������ʾ�����á��IJ��ֵ������
��2013•�����ض�ģ�����꼶��3������ĩ���Ժϸ����á�����ı�����1��6��3��С��ͬѧ����һ���뾶Ϊ2cm��Բ�ε�ͳ��ͼ����ͼ�������ʾ�����á��IJ��ֵ������| 12 |
| 5 |
| 12 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•�����ض�ģ����ͼ����֪����������y=
��2013•�����ض�ģ����ͼ����֪����������y=| m | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �������� | ���� ֱ�������� |
һֱ�DZ߳� | ��һֱ�� �߳� |
б�߳� | ||||||||
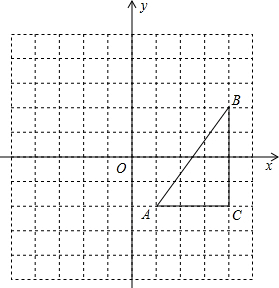
| A��1��-2�� B��4��2�� |
RT��ABC | AC=4-1=3 | BC=2-��-2�� | AB=
| ||||||||
| M��-4��2�� N��1��-3�� |
RT�� MPN MPN |
PN=1-��-4��=5 PN=1-��-4��=5 |
PM=2-��-3��=5 PM=2-��-3��=5 |
MN=
|
| (x-1)2+4 |
| (x-4)2+4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com