
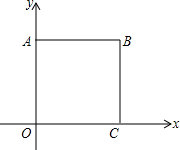
 ��ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������OABC���Ϊ16����E��A������ÿ��1����λ���ٶ����߶�AB���յ�B�˶���ͬʱ��F��A������ÿ��1����λ���ٶ����߶�AO���յ�O�˶�������ͬʱ�������˶�ʱ��Ϊt�룬һ�㵽���յ㣬����ͬʱֹͣ�˶���
��ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������OABC���Ϊ16����E��A������ÿ��1����λ���ٶ����߶�AB���յ�B�˶���ͬʱ��F��A������ÿ��1����λ���ٶ����߶�AO���յ�O�˶�������ͬʱ�������˶�ʱ��Ϊt�룬һ�㵽���յ㣬����ͬʱֹͣ�˶������� ��1���������ε��������������εı߳����Ӷ��õ���A�͵�C�����꣬Ȼ�����ô���ϵ�������AC�Ľ���ʽ���ɣ�
��2����ͼ1��ʾ����FC����֤����FOC�ա�EBC���Ӷ��õ���FCO=��ECB��Ȼ���ɡ�FOC+��FHC=180���֪F��O��C��H�ĵ㹲Բ�����ǵõ���FHO=��FCO�����������õȽǵ������ȿɵõ���OHC=��OCH���Ӷ���֤��OH=0C��
��3����֤��Rt��FOC��Rt��FHC���Ӷ��õ�CO=HC���ʴˡ�OHCΪ�ȱ������Σ����ǡ�FCO=30�㣬��������������Ǻ���ֵ�����OF=$\frac{4\sqrt{3}}{3}$��Ȼ�����AF�ij����Ӷ������t��ֵ��
��� �⣺��1����������OABC���Ϊ16��
��������OABC�ı߳���4��
��A�������ǣ�0��4����C�������ǣ�4��0����
��AC�Ľ���ʽ��y=kx+b��
��$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=4}\\{k=-1}\end{array}\right.$��
��AC�Ľ���ʽ��y=-x+4��
��2����ͼ1��ʾ������FC��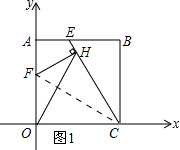
��AE=AF��AB=AO��
��OF=EB��
�ڡ�FOC�͡�EBC��$\left\{\begin{array}{l}{OF=BE}\\{��FOC=��EBC}\\{OC=BC}\end{array}\right.$��
���FOC�ա�EBC��
���FCO=��ECB��
��FH��EC��
���FHC=90�㣮
���FOC+��FHC=180�㣮
��F��O��C��H�ĵ㹲Բ��
���FHO=��FCO��
���FHO=��ECB��
�ߡ�FHO+OHC=90�㣬��ECB+��OCE=90�㣬
���OHC=��OCH��
��OH=0C��
��OH=4��
��3����ͼ2��ʾ������FC��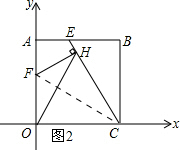
�ߡ�OFHΪ���������Σ�
��OF=FH��
��Rt��FOC��Rt��FHC��$\left\{\begin{array}{l}{FC=FC}\\{HF=OF}\end{array}\right.$��
��Rt��FOC��Rt��FHC��
��CO=HC����FCO=��FCH��
�ɣ�2����֪��OH=OC��
��OH=OC=CH��
���OCH=60�㣮
���FCO=30�㣮
��OF=$\frac{\sqrt{3}}{3}OC=\frac{\sqrt{3}}{3}��4$=$\frac{4\sqrt{3}}{3}$��
��AF=AO-OF=4$-\frac{4\sqrt{3}}{3}$=$\frac{12-4\sqrt{3}}{3}$��
��t=$\frac{12-4\sqrt{3}}{3}$��
���� ������Ҫ�������һ�κ����Ľ���ʽ�������ε����ʡ�ȫ�������ε����ʺ��ж������������ε��ж����ȱ������ε��ж���Բ�ܽǶ���������F��O��C��H�ĵ㹲Բ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ͼ�й���7�������Σ��ֱ��ǡ�ABC����ABE����BEC����DBO����EOC����BOC����ADE����A�ĶԱ���CD��CB��BE����CD���ԵĽ��ǡ�A����ABC��
��ͼ��ͼ�й���7�������Σ��ֱ��ǡ�ABC����ABE����BEC����DBO����EOC����BOC����ADE����A�ĶԱ���CD��CB��BE����CD���ԵĽ��ǡ�A����ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
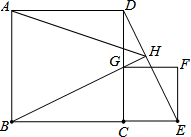 ����ͼ��������ABCD��G��CD���ϵ�һ�����㣨G����C��D�غϣ�����CGΪһ����������ABCD����������GCEF������DE��BG�����ӳ�BG��DE�ڵ�H��
����ͼ��������ABCD��G��CD���ϵ�һ�����㣨G����C��D�غϣ�����CGΪһ����������ABCD����������GCEF������DE��BG�����ӳ�BG��DE�ڵ�H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -10 | B�� | 4 | C�� | -4 | D�� | 10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com