
数学实验室:(本题12分)
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
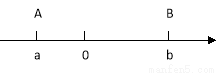
利用数形结合思想回答下列问题:
①数轴上表示2和5两点之间的距离是________,数轴上表示1和﹣3的两点之间的距离是________.(2分)
②数轴上表示 和
和 的两点之间的距离表示为__ ________.(3分)
的两点之间的距离表示为__ ________.(3分)
③若 表示一个有理数,且
表示一个有理数,且 ,化简:
,化简: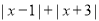 (4分)
(4分)
④若 表示一个有理数,且
表示一个有理数,且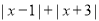 >4,则有理数
>4,则有理数 的取值范围是___________________(3分)
的取值范围是___________________(3分)
(1)3;4;(2)|x+2|;(3)4;(5)x>1或x<﹣3
【解析】
试题分析:①根据两点间距离公式求解即可;
②根据已知给出的求两点间距离的公式表示即可;
③根据x的取值范围,分别判断x﹣1与x+3的正负,然后根据绝对值的性质求解即可;
④根据已知的不等式进行分析,从而不难求得有理数x的取值范围.
试题解析:①∵2和5两点之间的距离是:|2﹣5|=3,1和﹣3的两点之间的距离是:|1﹣(﹣3)|=4,
∴数轴上表示2和5两点之间的距离是:3,数轴上表示1和﹣3的两点之间的距离是:4.
②∵x和﹣2的两点之间的距离为:|x﹣(﹣2)|=|x+2|,
∴数轴上表示x和﹣2的两点之间的距离表示为:|x+2|.
③∵﹣3<x<1,
∴|x﹣1|+|x+3|=1﹣x+x+3=4.
④当x>1时,原式=x﹣1+x+3=2x+2>4,解得,x>1;
当x<﹣3时,原式=﹣x+1﹣x﹣3=﹣2x﹣2>4,解得,x<﹣3;
当﹣3<x<1时,原式=﹣x+1+x+3=4,不符合题意,故舍去;
∴有理数x的取值范围是:x>1或x<﹣3.
考点:1.绝对值;22.数轴;3.代数式求值;4.解一元一次不等式.


科目:初中数学 来源:2014-2015学年江苏东台苏东双语八年级上学期第一次质检数学试卷(解析版) 题型:填空题
如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为 °.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏启东南苑中学七年级上学期第一单元测试数学试卷(解析版) 题型:选择题
冬季某天我国三个城市的最高气温分别是-10℃,1℃,-7℃,它们任意两城市中最大的温差是: ( )
A.11℃ B.17℃ C.8℃ D.3℃
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南京市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”,其中阴影部分面积为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南京市八年级上学期期中考试数学试卷(解析版) 题型:选择题
以下是甲、乙两人得到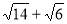 >
>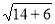 的推理过程:
的推理过程:
(甲)因为 ,
,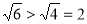 ,所以
,所以 , 又
, 又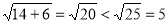 ,所以
,所以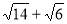 >
>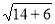 ;
;
(乙)作一个直角三角形,两直角边长分别为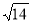 、
、 ,利用勾股定理得斜边长的平方为
,利用勾股定理得斜边长的平方为 ,因为斜边长大于0,故斜边长为
,因为斜边长大于0,故斜边长为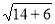 ,因为
,因为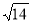 、
、 、
、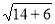 为三角形的三边长,所以
为三角形的三边长,所以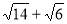 >
>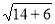 .对于两人的推理,下列说法正确的是( )
.对于两人的推理,下列说法正确的是( )
A.两人都正确 B.两人都错误
C.甲正确,乙错误 D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏江都区郭村一中七年级上学期第一次月考数学试卷(解析版) 题型:解答题
(本题8分)已知a、b互为相反数,m、n互为倒数,x 绝对值为2,求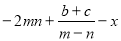 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏江都区郭村一中八年级上学期第一次月考数学试卷(解析版) 题型:解答题
(本题12分)在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,求证:△ABD≌△ACE.
(2)设∠BAC=α,∠BCE=β.
①如图1,当点D在线段BC上时,则α,β之间有怎样的数量关系?写出证明过程;
②当点D在直线BC上时,则α,β之间有怎样的数量关系?请画出图形并直接写出你的结论.


查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期中考试数学试卷(解析版) 题型:选择题
如果关于x的一元二次方程kx2-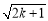 x+1=0有两个不相等的实数根,那么k的取值范围是
x+1=0有两个不相等的实数根,那么k的取值范围是
A.k< B.k<
B.k< 且k≠0
且k≠0
C.- ≤k<
≤k< D.-
D.- ≤k<
≤k< 且k≠0
且k≠0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com