Question

1．将△ABC沿BC方向平移到△A′B′C′，且BB′=n•BC，连AC′交A′B′于D，交A′B′于E．

（1）如图1，当n=2时，$\frac{DE}{AD}$=$\frac{2}{3}$，$\frac{EC'}{DE}$=$\frac{5}{4}$；
（2）如图2，当E为DC′的中点时，求证：n=$\sqrt{2}$+1；
（3）当n=$\frac{1+\sqrt{3}}{2}$或2+$\sqrt{6}$时，点E是C′D的三等分点．

Answer 1

分析 （1）根据已知条件可知BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，得$\frac{A′E}{AB}=\frac{ED}{AD}=\frac{2}{3}$，$\frac{CE}{CA}=\frac{1}{3}$即可解答．
（2）根据$\frac{AD}{DC}=\frac{AA′}{BC′}$得$\frac{n-1}{2}=\frac{n}{n+1}$，解方程即可．
（3）分EC′=2DE或DE=2EC′两种情形，通过比例式列出方程即可求出n．

解答 解：（1）如图1中，连接AA′，
∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，
∵BB′=2BC=2B′C′，
∴$\frac{B′E}{AB}$=$\frac{C′B′}{C′B}$=$\frac{1}{3}$，$\frac{CE}{AE}=\frac{C′B′}{B′B}$=$\frac{1}{2}$，
∴$\frac{A′E}{AB}=\frac{DE}{AD}$=$\frac{2}{3}$，$\frac{EC′}{DE}$=$\frac{5}{4}$，
故答案分别为$\frac{2}{3}$，$\frac{5}{4}$．
（2）∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，BB′=nBC，
∴$\frac{EC}{AE}=\frac{C′B′}{BB′}$=$\frac{1}{n}$，
∵DE=EC，
∴$\frac{AD}{DC}=\frac{AA′}{BC′}$，
∴$\frac{n-1}{2}=\frac{n}{n+1}$，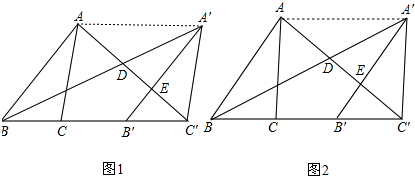
∴n²-2n-1=0
∴n=1+$\sqrt{2}$或1-$\sqrt{2}$
∵n＞0
∴n=1+$\sqrt{2}$．
（3）①当EC′=2DE时，
∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，
∴$\frac{EC′}{AE}=\frac{B′C′}{B′B}$=$\frac{1}{n}$，
∴$\frac{AD}{DC}$=$\frac{AA′}{BC′}$，
∴$\frac{n-\frac{1}{2}}{\frac{1}{2}+1}=\frac{n}{n+1}$，
整理得到2n²-2n-1=0
∴n=$\frac{1+\sqrt{3}}{2}$或$\frac{1-\sqrt{3}}{2}$（舍弃）．
②当DE=2EC′时，
∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，
∴$\frac{EC′}{AE}=\frac{B′C′}{B′B}$=$\frac{1}{n}$，
∴$\frac{AD}{DC}$=$\frac{AA′}{BC′}$，
∴$\frac{n-2}{2+1}=\frac{n}{n+1}$，
整理得到：n²-4n-2=0
∴n=2+$\sqrt{6}$或2-$\sqrt{6}$（舍弃）．
故答案为$\frac{1+\sqrt{3}}{2}$或2+$\sqrt{6}$．

点评 本题考查平移的性质、平行成比例等知识，图形比较复杂，灵活运用平行成比例是解决问题的关键，学会用方程的思想去解决问题．