练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    锐角△ABC中，sin B：sin C=m：n，则AB：AC=________．

    n：m
    分析：先过点A作BC的高，交BC与点D，则能写出sinB=，sinC=，再根据sin B：sin C=m：n，即可求出答案．
    解答：过点A作BC的高，交BC与点D，
    则sinB=，sinC=，
    又∵sin B：sin C=m：n，
    ∴=．
    故答案为n：m．
    点评：本题考查了锐角三角函数的定义，解题时牢记定义，并能灵活运用是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

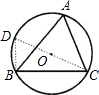    精英家教网阅读材料，解答问题：
    命题：如图，在锐角△ABC中，BC=a，CA=b，AB=c，△ABC的外接圆半径为R，则
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    =2R．
    证明：连接CO并延长交⊙O于点D，连接DB，则∠D=∠A．
    因为CD是⊙O的直径，所以∠DBC=90°，
    在Rt△DBC中，sin∠D=
    BC
    DC
    =
    a
    2R
    ，
    所以sinA=
    a
    2R
    ，即
    a
    sinA
    =2R，
    同理：
    b
    sinB
    =2R，
    c
    sinC
    =2R，
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    =2R，
    请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
    （1）前面阅读材料中省略了“
    b
    sinB
    =2R，
    c
    sinC
    =2R”的证明过程，请你把“
    b
    sinB
    =2R”的证明过程补写出来．
    （2）直接运用阅读材料中命题的结论解题，已知锐角△ABC中，BC=
    		3
    ，CA=
    		2
    ，∠A=60°，求△ABC的外接圆半径R及∠C．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    锐角△ABC中，sin B：sin C=m：n，则AB：AC=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省苏州工业园区九年级上学期期中测试数学卷 题型：选择题

     如果△ABC中，sin A＝cos B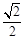＝，则下列最确切的结论是( ▲ )

    A．△ABC是直角三角形            B．△ABC是等腰三角形

    C．△ABC是等腰直角三角形        D．△ABC是锐角三角形

     

    查看答案和解析>>

    科目：初中数学 来源：2007年四川省自贡市富顺二中高一自主招生考试数学试卷（解析版） 题型：解答题

    阅读材料，解答问题：
    命题：如图，在锐角△ABC中，BC=a，CA=b，AB=c，△ABC的外接圆半径为R，则===2R．
    证明：连接CO并延长交⊙O于点D，连接DB，则∠D=∠A．
    因为CD是⊙O的直径，所以∠DBC=90°，
    在Rt△DBC中，sin∠D==，
    所以sinA=，即=2R，
    同理：=2R，=2R，===2R，
    请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
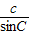    （1）前面阅读材料中省略了“=2R，=2R”的证明过程，请你把“=2R”的证明过程补写出来．
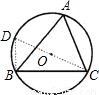
    （2）直接运用阅读材料中命题的结论解题，已知锐角△ABC中，BC=，CA=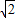，∠A=60°，求△ABC的外接圆半径R及∠C．


    查看答案和解析>>

    同步练习册答案