练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

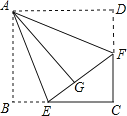
    【题目】如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长.

    【答案】

    【解析】分析：由正方形纸片ABCD的边长为3，可得∠C=90°，BC=CD=3，由根据折叠的性质得：EG=BE=1，GF=DF，然后设DF=x，在Rt△EFC中，由勾股定理EF2=EC2+FC2，即可得方程，解方程即可求得答案．

    详解∵正方形纸片ABCD的边长为3，∴∠C=90°，BC=CD=3.

    根据折叠的性质得：EG=BE=1，GF=DF.

    设DF=x，则EF=EG＋GF=1＋x，FC=DC－DF=3－x，EC=BC－BE=3－1=2.

    在Rt△EFC中，EF2=EC2＋FC2，即（x＋1）2=22＋（3－x）2，

    解得：.

    ∴DF= ，EF=1＋

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，以大于BF的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，得四边形ABEF.

    求证：四边形ABEF是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

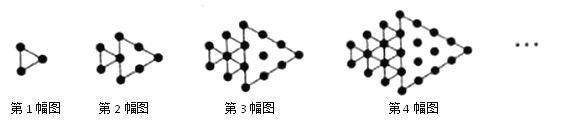
    【题目】如图所示，将形状、大小完全相同的“”和线段按照一定规律摆成下列图形.第1幅图形中“”的个数为，第2幅图形中“”的个数为，第3幅图形中“”的个数为，……，以此类推，解决以下问题：

    （1）直接写出 ， （用含n的代数式表示）；

    （2）猜想是否存在某幅图中“”的个数为2018，若存在，直接写出n的值；若不存在，则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数，并直接写出此时n的值；

    （3）求出的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

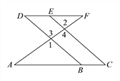
    【题目】如图，E点为DF上的点，B为AC上的点，，，求证：DF∥AC．

    证明：∵ （已知），∠1=∠3，∠2=∠4（ ），

    ∴∠3=∠4（等量代换）．

    ∴____________________（ ）．

    ∴∠C=∠ABD（ ）．

    ∵∠C=∠D（ ），

    ∴∠D=__________（ ）．

    ∴AC∥DF（ ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在BC上，且四边形AEFD是平行四边形．

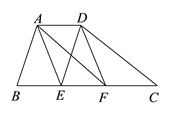
    （1）AD与BC有何等量关系？请说明理由；

    （2）当AB=DC时，求证：四边形AEFD是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则图中与∠DFM相等的角（不含它本身）的个数为（ ）

    A. 5 B. 6 C. 7 D. 8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

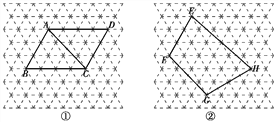
    【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.

    (1)边长为1的等边三角形的高=____;

    (2)图①中的ABCD的对角线AC的长=____;

    (3)图②中的四边形EFGH的面积=____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年，某市政府的一项实事工程就是由政府投入1 000万元资金，对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造，某社区为配合政府完成该项工作，对社区内1 200户家庭中的120户进行了随机抽样调查，并汇总成下表：

    改造情况

    均不改造

    改造水龙头

    改造马桶

    1个

    2个

    3个

    4个

    1个

    2个

    户数

    20

    31

    28

    21

    12

    69

    2

    (1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户；

    (2)改造后，一个水龙头一年大概可节约5吨水，一个马桶一年大约可节约15吨水，试估计该社区一年共可节约多少吨水？

    (3)在抽样的120户家庭中，既要改造水龙头又要改造马桶的家庭共有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级全体学生在5名教师的带领下去公园秋游，公园的门票为每人30元.现有两种优惠方案，甲方案：带队老师免费，学生按8折收费；乙方案：师生都按7.5折收费.

    （1）若有n名学生，用含n的代数式表示两种优惠方案各需多少元？

    （2）当n=70时，采用哪种方案更优惠？

    （3）当n=100时，采用哪种方案更优惠？

    查看答案和解析>>

    同步练习册答案