
分析 两种情况:①由矩形的性质得出CD=AB=8,BC=AD=10,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=10,由勾股定理求出DF,得出GF,即可求出AG;②同①得出AE=6,求出GE,即可得出AG的长,然后解直角三角形即可求得.
解答  解:分两种情况:①如图1所示:
解:分两种情况:①如图1所示:
∵四边形ABCD是矩形,
∴CD=AB=8,BC=AD=10,∠ADC=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=10,
∴DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=6,
∴AF=AD+DF=16,
∵G是EF的中点,
∴GF=$\frac{1}{2}$EF=5,
∴AG=AF-DF=16-5=11,
∴tan∠ABG=$\frac{AG}{AB}$=$\frac{11}{8}$;
②如图2所示:同①得:AE=6,
∵G是EF的中点,
∴GE=5,
∴AG=AE-GE=1,
∴tan∠ABG=$\frac{AG}{AB}$=$\frac{1}{8}$;
故答案为:$\frac{11}{8}$或$\frac{1}{8}$.
点评 本题考查了解直角三角形、矩形的性质、菱形的性质、勾股定理;熟练掌握矩形和菱形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{30}$天 | B. | $\frac{a}{60}$天 | C. | $\frac{a}{90}$天 | D. | $\frac{a}{180}$天 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
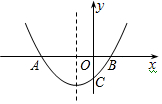 如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,∠OBC=45°,则下列各式成立的是( )
如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,∠OBC=45°,则下列各式成立的是( )| A. | 1-b+c=0 | B. | 1+b+c=0 | C. | 1+b-c=0 | D. | 1-b-c=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).
已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a=b,那么a+2b=3b | B. | 如果a=3,那么a-k=3-k | ||
| C. | 如果m=n,那么mc2=nc2 | D. | 如果mc2=nc2,那么m=n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
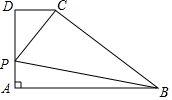 如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,CD=3,AB=9,AD=5,点P是腰AD上的一个动点,要使PC+PB最小,其最小值为( )
如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,CD=3,AB=9,AD=5,点P是腰AD上的一个动点,要使PC+PB最小,其最小值为( )| A. | 13 | B. | $\sqrt{13}$ | C. | $\sqrt{82}$ | D. | $\sqrt{85}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com