
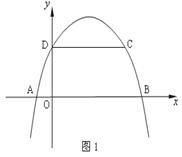
如图1,抛物线![]() 经过A(-1,0),C(3,2)两点,与
经过A(-1,0),C(3,2)两点,与![]() 轴交于点D,与
轴交于点D,与![]() 轴交于另一点B。
轴交于另一点B。
⑴求此抛物线的解析式;
⑵若直线![]() 将四边形ABCD面积二等分,求
将四边形ABCD面积二等分,求![]() 的值;
的值;
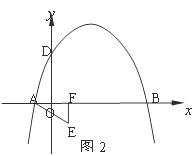
⑶如图2,过点E(1,-1)作EF⊥![]() 轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.
轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
 O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
 ),O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
),O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
查看答案和解析>>
科目:初中数学 来源:2013年安徽省中考数学模拟试卷(五)(解析版) 题型:解答题
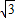 ),O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
),O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
查看答案和解析>>
科目:初中数学 来源:2009年初中毕业升学考试(安徽芜湖卷)数学(解析版) 题型:解答题
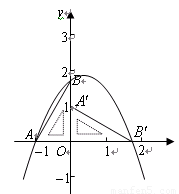
如图,在平面直角坐标系中放置一直角三角板,其顶点为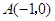 ,
,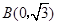 ,
,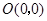 ,将此三角板绕原点
,将此三角板绕原点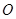 顺时针旋转
顺时针旋转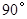 ,得到
,得到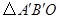 .
.
(1)如图,一抛物线经过点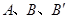 ,求该抛物线解析式;
,求该抛物线解析式;
(2)设点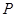 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形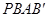 的面积达到最大时点
的面积达到最大时点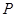 的坐标及面积的最大值.
的坐标及面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com