
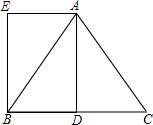 (2013•云南)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(2013•云南)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.科目:初中数学 来源:2012-2013学年江苏省兴化市九年级一模数学试卷(解析版) 题型:解答题
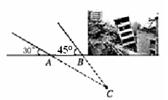
2013年3月10日,云南盈江县发生里氏5.8级地震。萧山金利浦地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象,已知废墟一侧地面上两探测点A、B 相距3米,探测线与地面的夹角分别是30°和45°(如图),试确定生命所在点C的深度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com