
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() Чв
Чв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
(1)ЧѓжЄ:![]() ;
;
(2)ШєСтаЮ![]() ЕФБпГЄЮЊ2,
ЕФБпГЄЮЊ2, ![]() .Чѓ
.Чѓ![]() ЕФГЄ.
ЕФГЄ.

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌдйИљОнСтаЮЕФЖдНЧЯпЛЅЯрДЙжБЧѓГіЁЯCOD=90ЁуЃЌжЄУїOCEDЪЧОиаЮЃЌПЩЕУOE=CDМДПЩЃЛ
ЃЈ2ЃЉИљОнСтаЮЕФаджЪЕУГіAC=ABЃЌдйИљОнЙДЙЩЖЈРэЕУГіAEЕФГЄЖШМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКдкСтаЮABCDжаЃЌOC=![]() ACЃЎ
ACЃЎ
ЁрDE=OCЃЎ
ЁпDEЁЮACЃЌ
ЁрЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЎ
ЁпACЁЭBDЃЌ
ЁрЦНааЫФБпаЮOCEDЪЧОиаЮЃЎ
ЁрOE=CDЃЎ
ЃЈ2ЃЉдкСтаЮABCDжаЃЌЁЯABC=60ЁуЃЌ
ЁрAC=AB=2ЃЎ
ЁрдкОиаЮOCEDжаЃЌ
CE=OD=![]() ЃЎ
ЃЎ
дкRtЁїACEжаЃЌ
AE=![]() ЃЎ
ЃЎ
ЕуОІЃКБОЬтПМВщСЫСтаЮЕФаджЪЃЌОиаЮЕФХаЖЈгыаджЪЃЌЙДЙЩЖЈРэЕФгІгУЃЌЪЧЛљДЁЬтЃЌЪьМЧОиаЮЕФХаЖЈЗНЗЈгыСтаЮЕФаджЪЪЧНтЬтЕФЙиМќЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓгывЛДЮКЏЪ§y=kx+bЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ6ЃЉЃЌЕуBЕФзјБъЮЊЃЈnЃЌ1ЃЉЃЎ
ЕФЭМЯѓгывЛДЮКЏЪ§y=kx+bЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ6ЃЉЃЌЕуBЕФзјБъЮЊЃЈnЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§гывЛДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉНсКЯЭМЯёаДГіВЛЕШЪН![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉЕуEЮЊyжсЩЯвЛИіЖЏЕуЃЌШєSЁїAEB=10ЃЌЧѓЕуEЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=![]() ,y=-
,y=-![]() x+7ЃЈ2ЃЉ0ЃМxЃМ2ЛђxЃО12ЃЈ3ЃЉЕуEЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЛђЃЈ0ЃЌ9ЃЉ
x+7ЃЈ2ЃЉ0ЃМxЃМ2ЛђxЃО12ЃЈ3ЃЉЕуEЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЛђЃЈ0ЃЌ9ЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)АбЕуAЕФзјБъДњШыЗДБШР§КЏЪ§НтЮіЪНЃЌЧѓГіЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌАбЕуBЕФзјБъДњШывбЧѓГіЕФЗДБШР§КЏЪ§НтЮіЪНЃЌЕУГіnЕФжЕ,ЕУГіЕуBЕФзјБъ,дйАбAЁЂBЕФзјБъДњШыжБЯп![]() ЃЌЧѓГіkЁЂbЕФжЕ,ДгЖјЕУГівЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЌЧѓГіkЁЂbЕФжЕ,ДгЖјЕУГівЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)ЩшЕуEЕФзјБъЮЊ(0,m)ЃЌСЌНгAEЃЌBEЃЌЯШЧѓГіЕуPЕФзјБъ(0,7)ЃЌЕУГіPE=|mЉ7|ЃЌИљОнSЁїAEB=SЁїBEPЉSЁїAEP=10ЃЌЧѓГіmЕФжЕЃЌДгЖјЕУГіЕуEЕФзјБъ.
НтЃКЃЈ1ЃЉАбЕуAЃЈ2ЃЌ6ЃЉДњШыy=![]() ЃЌЕУm=12ЃЌдђy=
ЃЌЕУm=12ЃЌдђy=![]() ЃЎ
ЃЎ
 АбЕуBЃЈnЃЌ1ЃЉДњШыy=
АбЕуBЃЈnЃЌ1ЃЉДњШыy=![]() ЃЌЕУn=12ЃЌдђЕуBЕФзјБъЮЊЃЈ12ЃЌ1ЃЉЃЎ
ЃЌЕУn=12ЃЌдђЕуBЕФзјБъЮЊЃЈ12ЃЌ1ЃЉЃЎ
гЩжБЯпy=kx+bЙ§ЕуAЃЈ2ЃЌ6ЃЉЃЌЕуBЃЈ12ЃЌ1ЃЉЃЌ
дђЫљЧѓвЛДЮКЏЪ§ЕФБэДяЪНЮЊy=Љ![]() x+7ЃЎ
x+7ЃЎ
ЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЌжБЯпABгыyжсЕФНЛЕуЮЊPЃЌЩшЕуEЕФзјБъЮЊЃЈ0ЃЌmЃЉЃЌСЌНгAEЃЌBEЃЌдђЕуPЕФзјБъЮЊЃЈ0ЃЌ7ЃЉЃЎЁрPE=|mЉ7|ЃЎ
ЁпSЁїAEB=SЁїBEPЉSЁїAEP=10ЃЌЁр![]() ЁС|mЉ7|ЁСЃЈ12Љ2ЃЉ=10ЃЎ
ЁС|mЉ7|ЁСЃЈ12Љ2ЃЉ=10ЃЎ
Ёр|mЉ7|=2ЃЎЁрm1=5ЃЌm2=9ЃЎЁрЕуEЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЛђЃЈ0ЃЌ9ЃЉЃЎ



 УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЁЧјЮЊСЫТЬЛЏЛЗОГЃЌМЦЛЎЗжСНДЮЙКНјAЁЂBСНжжЛЈВнЃЌЕквЛДЮЗжБ№ЙКНјAЁЂBСНжжЛЈВн30ПУКЭ15ПУЃЌЙВЛЈЗб675дЊЃЛЕкЖўДЮЗжБ№ЙКНјAЁЂBСНжжЛЈВн12ПУКЭ5ПУЃЎСНДЮЙВЛЈЗб940дЊЃЈСНДЮЙКНјЕФAЁЂBСНжжЛЈВнМлИёОљЗжБ№ЯрЭЌЃЉЃЎ
ЃЈ1ЃЉAЁЂBСНжжЛЈВнУППУЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШєЙКТђAЁЂBСНжжЛЈВнЙВ31ПУЃЌЧвBжжЛЈВнЕФЪ§СПЩйгкAжжЛЈВнЕФЪ§СПЕФ2БЖЃЌЧыФуИјГівЛжжЗбгУзюЪЁЕФЗНАИЃЌВЂЧѓГіИУЗНАИЫљашЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧвЛИіаТПюЫЎБЃЌЫЎБВЛЪЂЫЎЪБАДШчЭМ2ЫљЪОЕФЮЛжУЗХжУЃЌетбљПЩвдПьЫйСРИЩБЕзЃЌИЩОЛЭИЦјЃЛНЋЭМ2ЕФжїЬхВПЗжЕФГщЯѓГЩЭМ3ЃЌДЫЪББПкгыЫЎЦНжБЯпЕФМаНЧ35ЁуЃЌЫФБпаЮABCDПЩвдПДзїОиаЮЃЌВтЕУAB=10cmЃЌBC=8cmЃЌЙ§ЕуAзїAFЁЭCEЃЌНЛCEгкЕуFЃЎ 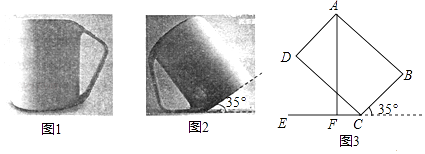
ЃЈ1ЃЉЧѓЁЯBAFЕФЖШЪ§ЃЛЃЈsin35ЁуЁж0.5736ЃЌcos35ЁуЁж0.8192ЃЌtan35ЁуЁж0.7002ЃЉ
ЃЈ2ЃЉЧѓЕуAЕНЫЎЦНжБЯпCEЕФОрРыAFЕФГЄЃЈОЋШЗЕН0.1cmЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛИљПЩЩьЫѕЕФгуИЭЃЌгуИЭЪЧгУ10НкДѓаЁВЛЭЌЕФПеаФЬзЙмСЌНгЖјГЩЃЎЯажУЪБгуИЭПЩЪеЫѕЃЌЭъШЋЪеЫѕКѓЃЌгуИЭГЄЖШМДЮЊЕк1НкЬзЙмЕФГЄЖШЃЈШчЭМ1ЫљЪОЃЉЃКЪЙгУЪБЃЌПЩНЋгуИЭЕФУПвЛНкЬзЙмЖМЭъШЋРЩьЃЈШчЭМ2ЫљЪОЃЉЃЎЭМ3ЪЧетИњгуИЭЫљгаЬзЙмЖМДІгкЭъШЋРЩьзДЬЌЯТЕФЦНУцЪОвтЭМЃЎвбжЊЕк1НкЬзЙмГЄ50cmЃЌЕк2НкЬзЙмГЄ46cmЃЌвдДЫРрЭЦЃЌУПвЛНкЬзЙмОљБШЧАвЛНкЬзЙмЩй4cmЃЎЭъШЋРЩьЪБЃЌЮЊСЫЪЙЯрСкСННкЬзЙмСЌНгВЂЙЬЖЈЃЌУПЯрСкСННкЬзЙмМфОљгаЯрЭЌГЄЖШЕФжиЕўЃЌЩшЦфГЄЖШЮЊxcmЃЎ

ЃЈ1ЃЉЧыжБНгаДГіЕк5НкЬзЙмЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБетИљгуИЭЭъШЋРЩьЪБЃЌЦфГЄЖШЮЊ311cmЃЌЧѓxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШЛЏМђ![]() ЁТЃЈ
ЁТЃЈ![]() Ѓ
Ѓ![]() ЃЉ,ШЛКѓдйДгЃ2ЃМxЁм2ЕФЗЖЮЇФкбЁШЁвЛИіКЯЪЪЕФxЕФећЪ§жЕДњШыЧѓжЕ
ЃЉ,ШЛКѓдйДгЃ2ЃМxЁм2ЕФЗЖЮЇФкбЁШЁвЛИіКЯЪЪЕФxЕФећЪ§жЕДњШыЧѓжЕ
ЁОД№АИЁП4.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЯШНЋдЗжЪННјааЛЏНтЃЌЛЏНтЙ§ГЬжазЂвтВЛЮЊ0ЕФСПЃЌИљОнВЛЮЊ0ЕФСПНсКЯxЕФШЁжЕЗЖЮЇЕУГіКЯЪЪЕФxЕФжЕЃЌНЋЦфДњШыЛЏМђКѓЕФДњЪ§ЪНжаМДПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃКдЪН= =
= =
=![]() ЃЎ
ЃЎ
Цфжа ЃЌМДxЁйЉ1ЁЂ0ЁЂ1ЃЎ
ЃЌМДxЁйЉ1ЁЂ0ЁЂ1ЃЎ
гжЁпЉ2ЃМxЁм2ЧвxЮЊећЪ§ЃЌЁрx=2ЃЎ
НЋx=2ДњШы![]() жаЕУЃК
жаЕУЃК ![]() =
=![]() =4ЃЎ
=4ЃЎ
ПМЕуЃКЗжЪНЕФЛЏМђЧѓжЕЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
21
ЁОЬтФПЁПНтЗНГЬЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЕуCЪЧЁбOЩЯвЛЕуЃЌADгыЙ§ЕуCЕФЧаЯпДЙжБЃЌДЙзуЮЊЕуDЃЌжБЯпDCгыABЕФбгГЄЯпЯрНЛгкЕуPЃЌЯвCEЦНЗжЁЯACBЃЌНЛABгкЕуFЃЌСЌНгBEЃЎ 
ЃЈ1ЃЉЧѓжЄЃКACЦНЗжЁЯDABЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїPCFЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉШєAF=6ЃЌEF=2 ![]() ЃЌЧѓЁбO ЕФАыОЖГЄЃЎ
ЃЌЧѓЁбO ЕФАыОЖГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуEЪЧBCЕФжаЕуЃЌСЌНгВЂбгГЄDEНЛABЕФбгГЄЯпгкЕуFЃЎ 
ЃЈ1ЃЉЧѓжЄЃКЁїCDEЁеЁїBFEЃЛ
ЃЈ2ЃЉШєCD=3cmЃЌЧыЧѓГіAFЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЫФБпаЮABCDЫФЬѕБпЩЯЕФжаЕуЗжБ№ЮЊEЁЂFЁЂGЁЂHЃЌЫГДЮСЌНгEFЁЂFGЁЂGHЁЂHEЃЌЕУЕНЫФБпаЮEFGHЃЈМДЫФБпаЮABCDЕФжаЕуЫФБпаЮЃЉЃЎ
ЃЈ1ЃЉЫФБпаЮEFGHЕФаЮзДЪЧ_____ЃЌ
жЄУїФуЕФНсТлЃЎ
ЃЈ2ЃЉЕБЫФБпаЮABCDЕФЖдНЧЯпТњзу_____ЬѕМўЪБЃЌЫФБпаЮEFGHЪЧОиаЮЃЛ
ЃЈ3ЃЉЕБЫФБпаЮABCDЕФЖдНЧЯпТњзу_____ЬѕМўЪБЃЌЫФБпаЮEFGHЪЧСтаЮЃЛ
ЃЈ4ЃЉФубЇЙ§ЕФФФжжЬиЪтЫФБпаЮЕФжаЕуЫФБпаЮЪЧОиаЮЃП_____ЃЛ
ЃЈ5ЃЉФубЇЙ§ЕФФФжжЬиЪтЫФБпаЮЕФжаЕуЫФБпаЮЪЧСтаЮЃП_____ЃЛ
ЃЈ6ЃЉФубЇЙ§ЕФФФжжЬиЪтЫФБпаЮЕФжаЕуЫФБпаЮЪЧе§ЗНаЮЃП_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМКжЊвЛдЊЖўДЮЗНГЬx2Љ3x+mЉ1=0ЃЎ
ЃЈ1ЃЉШєЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЗНГЬгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЧѓДЫЪБЗНГЬЕФИљЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com