
如图,正方形ABCD的面积为S,对角线相交于点O,点O是正方形![]() 的一个顶点,如果两个正方形的边长相等,那么正方形
的一个顶点,如果两个正方形的边长相等,那么正方形![]() 绕点O转动时,
绕点O转动时,
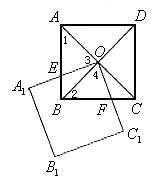
(1)求两个正方形重叠部分的面积。
(2)如果正方形![]() 的边长大于正方形ABCD的边长,则重叠部分的面积等于多少?与上述结论是否一致?
的边长大于正方形ABCD的边长,则重叠部分的面积等于多少?与上述结论是否一致?
(3)将正方形![]() 改为
改为![]() ,只要满足什么条件,重叠部分的面积不变?
,只要满足什么条件,重叠部分的面积不变?
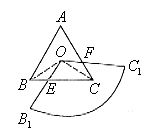
(4)如果把正方形ABCD改为等边△ABC,O为等边△ABC的中心,以O为顶点的扇形![]() 绕点O无论怎样转动,要使它与等边△ABC的重叠部分的面积总保持不变,问扇形
绕点O无论怎样转动,要使它与等边△ABC的重叠部分的面积总保持不变,问扇形![]() 应满足什么条件?并且说明你的理由。
应满足什么条件?并且说明你的理由。
(1)解:∵ABCD为正方形
∴OA=OB,AC⊥BD
∠1=∠2=45°
∠3+∠BOE=90°
∵![]() 是正方形
是正方形
∴∠BOE+∠4=90°
∴∠3=∠4
∴△AOE≌△BOF
![]()
∴两个正方形重叠部分的面积![]()
(2)如果正方形![]() 的边长大于正方形ABCD的边长,则重叠部分的面积仍然等于
的边长大于正方形ABCD的边长,则重叠部分的面积仍然等于![]() 与上述结论一致。因为求解的过程没有任何改变。
与上述结论一致。因为求解的过程没有任何改变。
(3)将正方形![]() 变为
变为![]() ,只要满足
,只要满足![]() ,并且
,并且![]() 与正方形ABCD没有交点,那么求重叠部分的面积的方法与上面的方法一样,所以重叠部分的面积不改变。
与正方形ABCD没有交点,那么求重叠部分的面积的方法与上面的方法一样,所以重叠部分的面积不改变。
(4)如果把正方形ABCD改为等边△ABC,O为等边△ABC的中心,以O为顶点的扇形![]() 绕点O无论怎样转动,要使它与等边△ABC的重叠部分的面积总保持不变,扇形
绕点O无论怎样转动,要使它与等边△ABC的重叠部分的面积总保持不变,扇形![]() 应满足的条件是:
应满足的条件是:
![]() ,且
,且![]()
类似上面的方法,容易证明△BOE≌△COF(如图4)。
所以重叠部分的面积![]() ,而且保持不变。
,而且保持不变。


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com