
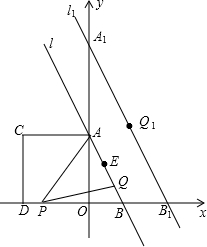
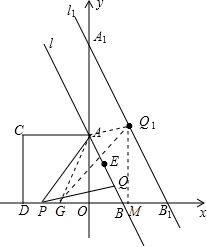
 ��ͼ��ֱ��l��y=-2x+4��y����A�㣬��x����B�㣬�ı���OACDΪ�����Σ���P��D�㿪ʼ��x�����O��ÿ��2����λ���ٶ��ƶ�����Q�ӵ�B��ʼ��BA���A��ÿ��
��ͼ��ֱ��l��y=-2x+4��y����A�㣬��x����B�㣬�ı���OACDΪ�����Σ���P��D�㿪ʼ��x�����O��ÿ��2����λ���ٶ��ƶ�����Q�ӵ�B��ʼ��BA���A��ÿ�� ����λ���ٶ��ƶ������P��Q�ֱ��D��Bͬʱ������
����λ���ٶ��ƶ������P��Q�ֱ��D��Bͬʱ������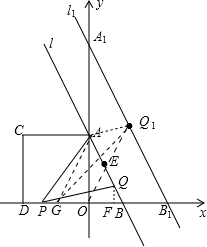 �⣺��1����ֱ��l��y=-2x+4��y����A�㣬��x����B�㣬
�⣺��1����ֱ��l��y=-2x+4��y����A�㣬��x����B�㣬 t��
t��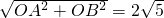 ��
��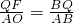 ��
��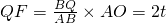 ��
��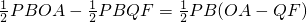 ��
��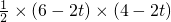 ��
��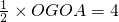 ��
��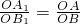 ��
��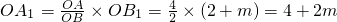 ��
��
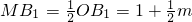 ��
��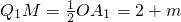 ��
��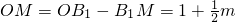 ��
��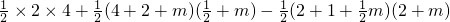
 t����Rt��AOB�У����AB�ij��ȣ���QF��OB��F��������������֤����QFB�ס�AOB����t��ʾ��QF��S=S��PBA-S��PBQ���������S��t֮��ĺ�����ϵ��
t����Rt��AOB�У����AB�ij��ȣ���QF��OB��F��������������֤����QFB�ס�AOB����t��ʾ��QF��S=S��PBA-S��PBQ���������S��t֮��ĺ�����ϵ��

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 13����ͼ��ֱ��a��b����ֱ��c�ཻ������������������1����l=��2����2����3=��6����3����4+��7=180�㣻��4����5+��8=180�㣬�������ж�a��b���ǣ�������
13����ͼ��ֱ��a��b����ֱ��c�ཻ������������������1����l=��2����2����3=��6����3����4+��7=180�㣻��4����5+��8=180�㣬�������ж�a��b���ǣ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 4����ͼ��ֱ��AB��CD�ཻ�ڵ�E��EF��AB��E������CEF=59�㣬���AED�Ķ���Ϊ��������
4����ͼ��ֱ��AB��CD�ཻ�ڵ�E��EF��AB��E������CEF=59�㣬���AED�Ķ���Ϊ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ֱ��y=6-x��x�ᡢy����A��B���㣬P�Ƿ���������y=
��ͼ��ֱ��y=6-x��x�ᡢy����A��B���㣬P�Ƿ���������y=| 4 |
| x |
| A��8 | ||
| B��6 | ||
| C��4 | ||
D��6
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 17����ͼ��ֱ��a��c��b��c��ֱ��d��ֱ��a��b��c�ཻ����֪��1=60�㣬���2����3�Ķ���������ͼ�������ֱ�ʾ�ǣ���
17����ͼ��ֱ��a��c��b��c��ֱ��d��ֱ��a��b��c�ཻ����֪��1=60�㣬���2����3�Ķ���������ͼ�������ֱ�ʾ�ǣ����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com