
如图,已 知直线 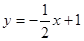 交坐标轴于
交坐标轴于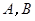 两点,以线段
两点,以线段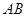 为边向上作正方形
为边向上作正方形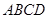 ,过点
,过点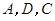 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为 .
.

(1)请直接写出点 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒 个单位长度的速度沿射线
个单位长度的速度沿射线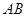 下滑,直至顶点
下滑,直至顶点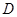 落在x轴上时停止.设正方形落在
落在x轴上时停止.设正方形落在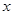 轴下方部分的面积为
轴下方部分的面积为 ,求
,求 关于滑行时间
关于滑行时间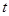 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量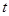 的取值范围;
的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上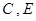 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.
(1)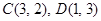 (2)
(2)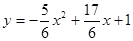 .
.
(3)当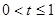 时,
时,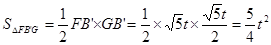
当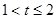 时,S=
时,S=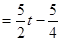
当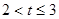 时,S=
时,S=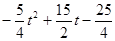 (4)
(4) 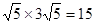
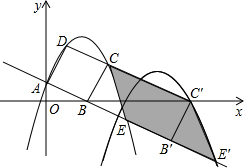
【解析】(1)可先根据AB所在直线的解析式求出A,B两点的坐标,即可得出OA、OB的长.过D作DM⊥y轴于M,则△ADM≌△BAO,由此可得出MD、MA的长,也就能求出D的坐标,同理可求出C的坐标;
(2)可根据A、C、D三点的坐标,用待定系数法求出抛物线的解析式;
(3)要分三种情况进行讨论:
①当F点在A′B′之间时,即当0<t≤1时,此时S为三角形FBG的面积,可用正方形的速度求出AB′的长,即可求出B′F的长,然后根据∠GFB′的正切值求出B′G的长,即可得出关于S、t的函数关系式.
②当A′在x轴下方,但C′在x轴上方或x轴上时,即当1<t≤2时,S为梯形A′GB′H的面积,可参照①的方法求出A′G和B′H的长,那么梯形的上下底就可求出,梯形的高为A′B′即正方形的边长,可根据梯形的面积计算公式得出关于S、t的函数关系式.
③当D′逐渐移动到x轴的过程中,即当2<t≤3时,此时S为五边形A′B′C′HG的面积,S=正方形A′B′C′D′的面积-三角形GHD′的面积.可据此来列关于S,t的函数关系式;
(4)CE扫过的图形是个平行四边形,经过关系不难发现这个平行四边形的面积实际上就是矩形BCD′A′的面积.可通过求矩形的面积来求出CE扫过的面积


科目:初中数学 来源: 题型:解答题
 如图,已知直线
如图,已知直线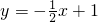 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分12分)如图,已知直线![]() 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.

1.(1)填空:点A的坐标为 ,点B的坐标为 ,AB的长为 .
2.(2)求点C、D的坐标
3.(3)求抛物线的解析式
4.(4)若抛物线与正方形沿射线AB下滑,直至点C落在![]() 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省惠州市惠城区十一校九年级上学期期末联考数学卷 题型:解答题
如图,已知直线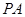 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O 上一点,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O 上一点,过C作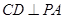 ,垂足为D。问:当AC满足什么条件时,CD为⊙O的切线,请说明理由。
,垂足为D。问:当AC满足什么条件时,CD为⊙O的切线,请说明理由。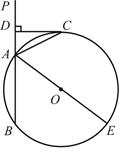
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建省厦门市翔安区九年级适应性考试数学卷(解析版) 题型:解答题
(1)如图,已知线段AB,请用直尺和圆规作出线段AB的垂直平分线(不写画法,保留作图痕迹);

(2)计算: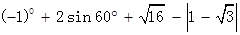
(3)如图,已知 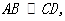 直线
直线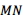 交
交 于
于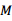 ,交
,交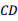 于
于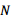 ,
,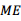 平分
平分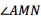 ,
,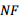 平分
平分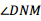
求证: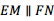
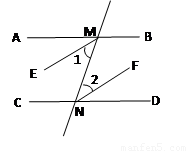
查看答案和解析>>
科目:初中数学 来源:2011年河北省中考考前模拟测试数学卷(3) 题型:解答题
如图,已知直线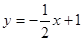 交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
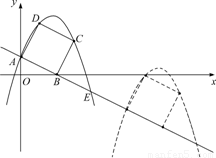
1.请直接写出点C,D的坐标;
2.求抛物线的解析式
3.若正方形以每秒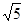 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围
4.在(3)的条件下,抛物线与正方形一起平移,同时D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com