练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线y=ax2+bx+c（a＞0）的对称轴为直线x=1，且经过点（﹣1，y1），（﹣2，y2），试比较y1和y2的大小：y1____y2（填“＞”，“＜”或“=”）．

    【答案】＜

    【解析】分析：比较三个点离直线x=1的远近即可得到y1、y2的大小关系．

    详解：∵抛物线y=ax2+bx+c（a＞0）的对称轴为直线x=1，且经过点（-1，y1），（-2，y2），

    ∴点（-1，y1）直线x=1最近，点（-2，y2）离直线x=1最远，

    ∵抛物线开口向上，

    ∴y1＜y2．

    故答案为：＜．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

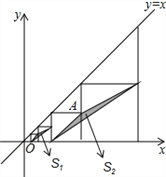
    【题目】如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn，则Sn的值为__．（用含n的代数式表示，n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标都在格点上，且△A1B1C1与△ABC关于原点O成中心对称，C点坐标为（-2,1）。

    （1）请直接写出A1的坐标　 　；并画出△A1B1C1．

    （2）P（a，b）是△ABC的AC边上一点，将△ABC平移后点P的对称点P'（a+2，b﹣6），请画出平移后的△A2B2C2．

    （3）若△A1B1C1和△A2B2C2关于某一点成中心对称，则对称中心的坐标为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，AB=BD，点E、F分别在BC、CD上，且BE=CF，连接BF、DE交于点M，延长ED到H使DH=BM，连接AM，AH，则以下四个结论：

    ①△BDF≌△DCE；②∠BMD=120°；③△AMH是等边三角形；④S四边形ABCD= AM2．

    其中正确结论的个数是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

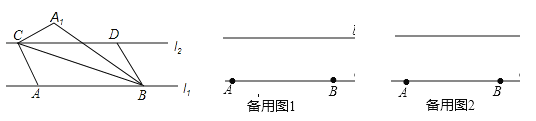
    【题目】已知：直线l1与直线l2平行，且它们之间的距离为2，A、B是直线l1上的两个定点，C、D是直线l2上的两个动点（点C在点D的左侧），AB=CD=5，连接AC、BD、BC，将△ABC沿BC折叠得到△A1BC．

    （1）求四边形ABDC的面积．

    （2）当A1与D重合时，四边形ABDC是什么特殊四边形，为什么？

    （3）当A1与D不重合时：①连接A1、D，求证：A1D∥BC；②若以A1，B，C，D为顶点的四边形为矩形，且矩形的边长分别为a，b，求（a+b）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列性质中，平行四边形不一定具备的是（ ）
    A.邻角互补
    B.对角互补
    C.对边相等
    D.对角线互相平分

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为计算简便,把(-2.4)-(-4.7)-(+0.5)+(+3.4)+(-3.5)写成省略加号的和的形式,并按要求交换加数的位置正确的是( ).

    A. -2.4+3.4-4.7-0.5-3.5

    B. -2.4+3.4+4.7+0.5-3.5

    C. -2.4+3.4+4.7-0.5-3.5

    D. -2.4+3.4+4.7-0.5+3.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的有（　　）

    ①所有的有理数都能用数轴上的点表示；

    ②符号不同的两个数互为相反数；

    ③有理数分为正数和负数；

    ④两数相减，差一定小于被减数；

    ⑤两数相加，和一定大于任何一个加数．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

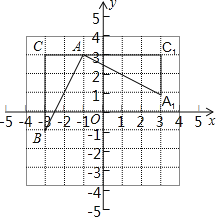
    【题目】如图，在平面直角坐标系中，有一Rt△ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．

    （1）请写出旋转中心的坐标是 ，旋转角是 度；

    （2）以（1）中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°、180°的三角形；

    （3）设Rt△ABC两直角边BC=a、AC=b、斜边AB=c，利用变换前后所形成的图案证明勾股定理．

    查看答案和解析>>

    同步练习册答案