
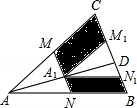
 如图,如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置,且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为14.
如图,如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置,且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为14. 分析 根据三角形中位线定理得到MN∥BC,MN=$\frac{1}{2}$BC,得到△AMN∽△ACB,根据相似三角形的性质和平移的性质计算即可.
解答 解:∵M、N分别是△ABC的边AC和AB的中点,
∴MN∥BC,MN=$\frac{1}{2}$BC,
∴△AMN∽△ACB,相似比为1:4,
∵△AMN的面积为7,
∴△ABC的面积为28,
由平移的性质可知,△AMN的面积=△A1M1N1的面积=7,
∴图中阴影部分的面积为28-7-7=14,
故答案为:14.
点评 本题考查的是三角形中位线定理和相似三角形的性质以及平移的性质,三角形的中位线平行于第三边,并且等于第三边的一半、把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D.
如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com