
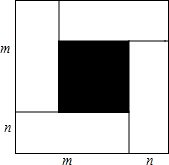
 如图,大正方形由四个相同的长方形和一个小正方形组成,设长方形的两边长为m,n(m>n),大小正方形的边长分别为x,y.观察图案,指出以下关系式:①x2-y2=4mn;②m2-n2=xy;③2n2=(x-y)2;④m2+n2=$\frac{{x}^{2}+{y}^{2}}{2}$,其中正确的是①②④(写出正确结论的序号)
如图,大正方形由四个相同的长方形和一个小正方形组成,设长方形的两边长为m,n(m>n),大小正方形的边长分别为x,y.观察图案,指出以下关系式:①x2-y2=4mn;②m2-n2=xy;③2n2=(x-y)2;④m2+n2=$\frac{{x}^{2}+{y}^{2}}{2}$,其中正确的是①②④(写出正确结论的序号) 分析 根据长方形的长和宽,结合图形进行判断,即可求解.
解答 解:由图形可知:大正方的面积-小正方形的面积=4×长方形的面积,即x2-y2=4mn,故①正确,
∵大正方形的边长x=m+n,小正方形的面积y=m-n,
∴(m+n)(m-n)=xy,即m2-n2=xy,故②正确,
∵x-y=2n,
∴4n2=(x-y)2;故③错误;
∵(m+n)2=x2,(m-n)2=y2,
∴两式相加可得m2+n2=$\frac{{x}^{2}+{y}^{2}}{2}$,故④正确.
∴正确的为①②④.
故答案为:①②④.
点评 本题考查了完全平方公式的几何背景及因式分解的应用,主要考查学生的计算能力和观察图形的能力.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)| 项目 人员 | 教学能力 | 科研能力 | 组织能力 |
| 甲 | 86 | 93 | 73 |
| 乙 | 81 | 95 | 79 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com