
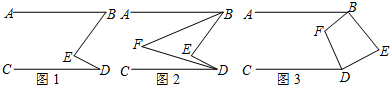
分析 (1)首先作EF∥AB,根据直线AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,据此推得∠ABE+∠CDE=∠BED即可.
(2)首先根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CDF=$\frac{1}{2}$(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=$\frac{1}{2}$∠BED.
(3)首先过点E作EG∥CD,再根据AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,据此推得∠ABE+∠CDE+∠BED=360°;然后根据∠BFD=∠ABF+∠CDF,以及BF,DF分别平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
解答 解:(1)如图1,作EF∥AB,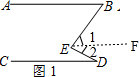 ,
,
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
(2)如图2,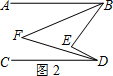 ,
,
∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=$\frac{1}{2}$∠ABE,∠CDF=$\frac{1}{2}$∠CDE,
∴∠ABF+∠CDF=$\frac{1}{2}$∠ABE+$\frac{1}{2}$∠CDE=$\frac{1}{2}$(∠ABE+∠CDE)
由(1),可得
∠BFD=∠ABF+∠CDF=$\frac{1}{2}$(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=$\frac{1}{2}$∠BED.
(3)如图3,过点E作EG∥CD,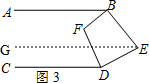 ,
,
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=$\frac{1}{2}$∠ABE,∠CDF=$\frac{1}{2}$∠CDE,
∴∠BFD=$\frac{1}{2}$(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:∠ABE+∠CDE=∠BED、∠BFD=$\frac{1}{2}$∠BED.
点评 此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.②定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 明天我市下雨 | |
| B. | 抛一枚硬币,正面朝下 | |
| C. | 购买一张福利彩票中奖了 | |
| D. | 掷一枚骰子,向上一面的数字一定大于零 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABD,△BCE均为等边三角形,A,B,C三点在同一直线上,点F在AB上,且∠DFE=60°,以下结论:①DF=EF;②AF=BC;③$\frac{FB}{BC}$=$\frac{BE}{DF}$;④DF2=DB•DG,正确的有(填序号)①②④.
如图,△ABD,△BCE均为等边三角形,A,B,C三点在同一直线上,点F在AB上,且∠DFE=60°,以下结论:①DF=EF;②AF=BC;③$\frac{FB}{BC}$=$\frac{BE}{DF}$;④DF2=DB•DG,正确的有(填序号)①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
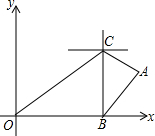 中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{5}{3}}$=$\frac{1}{3}$$\sqrt{5}$ | B. | $\sqrt{54}$•$\sqrt{\frac{1}{2}}$=$\frac{3}{2}\sqrt{6}$ | C. | $\frac{\sqrt{24}}{\sqrt{3}}$=$\sqrt{2}$ | D. | 3$\sqrt{2a}$-$\sqrt{8a}$=$\sqrt{2a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com