练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （12分）如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=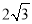，其中∠BAC=90°，将△ABC绕点P旋转180°，得到△MCB．

    （1）求B、C两点的坐标；

    （2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；

    （3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016届辽宁省灯塔市九年级上学期期中考试数学试卷（解析版） 题型：填空题

    如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AD＝3，DB=2，BC＝6，则DE的长为 ．

    查看答案和解析>>

    科目：初中数学 来源：2016届江苏省盐城市九年级上学期期中考试数学试卷（解析版） 题型：解答题

    （本题满分12分）已知，△ABC在平面直角坐标系中的位置如图①所示，A点坐标为（－6，0），B点坐标为（4，0），点D为BC的中点，点E为线段AB上一动点,。经过点A、B、C三点的抛物线的解析式为y＝ax2＋bx＋8．

    （1）求抛物线的解析式；

    （2）如图①，连接DE，将△BDE以DE为轴翻折，点B的对称点为点G，当点G恰好落在抛物线的对称轴上时，求G点的坐标；

    （3）如图②，连接AD，点F是抛物线上A、C之间的一点，直线BF交AD于点P，连接PE, 试探索BP＋PE是否存在最小值？若存在，求出这个最小值，并直接写出此时点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2016届江苏省盐城市九年级上学期期中考试数学试卷（解析版） 题型：填空题

    近年来食品安全问题备受人们的关注，某海关想检验一批进口食品的防腐剂含量是否符合国家标准，这种调查适用 （填“全面调查”或“抽样调查”）．

    查看答案和解析>>

    科目：初中数学 来源：2016届江苏省盐城市九年级上学期期中考试数学试卷（解析版） 题型：选择题

    若x＞y，则下列式子错误的是（ ）

    A、x－3＞y－3 B、－3x＞－3y C、x＋3＞y＋3 D、

    查看答案和解析>>

    科目：初中数学 来源：2016届江苏省九年级上学期第一次月考数学试卷（解析版） 题型：解答题

    （9分）如图所示，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D．已知：AB=24cm，CD=8cm．

    （1）求作此残片所在的圆（不写作法，保留作图痕迹）；

    （2）求（1）中所作圆的半径．

    查看答案和解析>>

    科目：初中数学 来源：2016届江苏省九年级上学期第一次月考数学试卷（解析版） 题型：填空题

    直角三角形的两边长分别为16和12，则此三角形的外接圆的半径是 ．

    查看答案和解析>>

    科目：初中数学 来源：2016届湖北省武汉市东西湖区九年级上学期期中考试数学试卷（解析版） 题型：解答题

    某公司拟用运营指数y来量化考核司机的工作业绩，运营指数（y）与运输次数（n）和平均速度（x）之间满足关系式为y=ax2＋bnx＋100，当n=1,x=30时，y=190；当n=2，x=40时，y=420

    用含x和n的式子表示y；

    当运输次数定为3次，求获得最大运营指数时的平均速度；

    若n=2,x=40,能否在n增加m%（m＞0）,同时x减少m%的情况下，而y的值保持不变，若能，求出m的值；若不能，请说明理由。

    参考公式：抛物线y=ax2＋bx＋c（a≠0）的顶点坐标是（－，）

    查看答案和解析>>

    科目：初中数学 来源：2015-2016学年内蒙古乌海市八年级上学期期中考试数学试卷（解析版） 题型：选择题

    一个三角形任意一边上的高都是这边上的中线，则对这个三角形最准确的判断是（ ）

    A．等腰三角形 B．直角三角形 C．正三角形 D．等腰直角三角形

    查看答案和解析>>

    同步练习册答案