在直角坐标系内有两点A(-1,1)、B(2,3),若M为x轴上一点,且MA+MB最小,则M的坐标是 ,MA+MB= .
【答案】
分析:取点A关于x轴的对称点A′(-1,-1),连接A′B,已知两点坐标,可用待定系数法求出直线A′B的解析式,从而确定出占M的坐标;再两点间的距离公式求得A'B的值即为MA+MB的值.
解答:解:取点A关于x轴的对称点A′(-1,-1),连接A′B,
∵A′(-1,-1),B(2,3),
设直线A'B的解析式为y=kx+b,
由有:
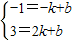
,
解得:k=

,b=

,
∴直线A′B的解析式为:y=

x+

,
当y=0时,x=-

,
即M(-

,0);
A'B=
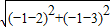
=5,此时MA+MB=A′B=5为最小.
故本题答案为:(-

,0);5.
点评:利用轴对称找线段和的最小值,如果所求的点在x轴上,就取x轴的对称点,如果所求的点在y轴上,就取y轴的对称点,求直线解析式,确定直线与坐标轴的交点,即为所求.

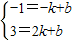 ,
, ,b=
,b= ,
, x+
x+ ,
, ,
, ,0);
,0);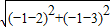 =5,此时MA+MB=A′B=5为最小.
=5,此时MA+MB=A′B=5为最小. ,0);5.
,0);5.
