
【题目】我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
【答案】(1)见解析;(2)144°;(3)众数为1.5小时、中位数为1.5小时.
【解析】
试题分析:(1)根据学生劳动“1小时”的人数除以占的百分比,求出总人数,
(2)进而求出劳动“1.5小时”的人数,以及占的百分比,乘以360即可得到结果;
(3)根据统计图中的数据确定出学生劳动时间的众数与中位数即可.
解:(1)根据题意得:30÷30%=100(人),
∴学生劳动时间为“1.5小时”的人数为100﹣(12+30+18)=40(人),
补全统计图,如图所示:
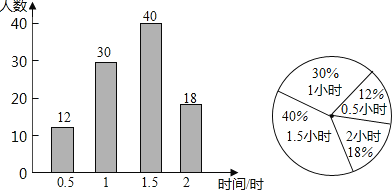
(2)根据题意得:40%×360°=144°,
则扇形图中的“1.5小时”部分圆心角是144°;
(3)根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
分组 | 划记 | 频数 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 6.5<x≤8.0 | ||
8.0<x≤9.5 合计 |
| 2 50 |

(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题属于定义的是( )
A. 两点之间线段最短
B. 25的平方根是±5
C. 同旁内角互补
D. 含有两个未知数,并且未知数的次数是1的整式方程是二元一次方程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)某合作学习小组的6名同学在一次数学测试中,成绩分布为76,88,96,82,78,96,这组数据的中位数是( )
A.82 B.85 C.88 D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知二次函数![]() 的图像如图,请根据图像直接写出该二次函数图像经过怎样的左右平移,新图像通过坐标原点?
的图像如图,请根据图像直接写出该二次函数图像经过怎样的左右平移,新图像通过坐标原点?
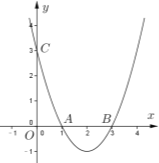
(2)在关于二次函数图像的研究中,秦篆晔同学发现抛物线![]() (
(![]() )和抛物线
)和抛物线![]() (
(![]() )关于
)关于![]() 轴对称,基于协作共享,秦同学将其发现口诀化“
轴对称,基于协作共享,秦同学将其发现口诀化“![]() 、
、![]() 不变,
不变,![]() 相反”供大家分享,而在旁边补笔记的胡庄韵同学听成了“
相反”供大家分享,而在旁边补笔记的胡庄韵同学听成了“![]() 、
、![]() 相反,
相反,![]() 不变”,并按此法误写,然而按此误写的抛物线恰巧与原抛物线也对称,请你写出小胡同学所写的与原抛物线
不变”,并按此法误写,然而按此误写的抛物线恰巧与原抛物线也对称,请你写出小胡同学所写的与原抛物线![]() 的对称图形的解析式,并研究其与原抛物线的具体对称情况;
的对称图形的解析式,并研究其与原抛物线的具体对称情况;
(3)抛物线![]() 与
与![]() 轴从左到右交于
轴从左到右交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 是其对称轴上一点,点
是其对称轴上一点,点![]() 在
在![]() 轴上,当点
轴上,当点![]() 满足怎样的条件,以点
满足怎样的条件,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 有可能相似,请写出所有满足条件的点
有可能相似,请写出所有满足条件的点![]() 的坐标;
的坐标;
(4)![]() 、
、![]() 为抛物线
为抛物线![]() 上两点,且
上两点,且![]() 、
、![]() 关于
关于![]() 对称,请直接写出
对称,请直接写出![]() 、
、![]() 两点的坐标;
两点的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com