
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
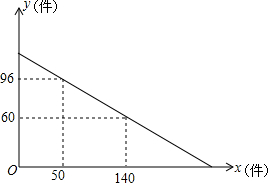 某服装店老板到批发中心批发A,B两种新款上衣,A种上衣的进货单价是B种上衣进货单价的1.5倍,考虑到各种因素,预计批发A种上衣数量y(件)与B种上衣的数量x(件)之间的函数关系如图所示,已知若批发的A,B 两种上衣中,A种有80件时,A,B两种上衣共需16800元.
某服装店老板到批发中心批发A,B两种新款上衣,A种上衣的进货单价是B种上衣进货单价的1.5倍,考虑到各种因素,预计批发A种上衣数量y(件)与B种上衣的数量x(件)之间的函数关系如图所示,已知若批发的A,B 两种上衣中,A种有80件时,A,B两种上衣共需16800元. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com