
科目:初中数学 来源: 题型:选择题
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 在同一平面内,a⊥b,b⊥c,则c⊥a | |
| C. | 同旁内角互补,则它们的角平分线互相垂直 | |
| D. | 经过一点有且只有一条直线与已知直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
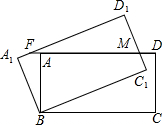 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为=2-$\sqrt{3}$.
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为=2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
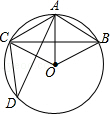 如图,在半径为6 cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BDC}$上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3$\sqrt{3}{cm}$;③∠AOB=60°;④四边形ABOC是菱形,其中正确结论的序号是①③④.
如图,在半径为6 cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BDC}$上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3$\sqrt{3}{cm}$;③∠AOB=60°;④四边形ABOC是菱形,其中正确结论的序号是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
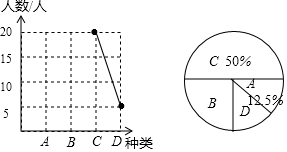 巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题:
巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 两转盘颜色(甲,乙) | (黑,黑) | (黑,白) | (白,黑) | (白,白) |
| 中奖金额 | 0元 | 1元 | 2元 | 3元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com