
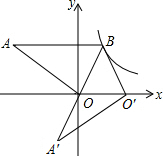
 如图,△AOB,AB∥x轴,OB=2,点B在反比例函数y=$\frac{k}{x}$上,将△AOB绕点B逆时针旋转,当点O的对应点O′落在x轴的正半轴上时,AB的对应边A′B恰好经过点O,则k的值为$\sqrt{3}$.
如图,△AOB,AB∥x轴,OB=2,点B在反比例函数y=$\frac{k}{x}$上,将△AOB绕点B逆时针旋转,当点O的对应点O′落在x轴的正半轴上时,AB的对应边A′B恰好经过点O,则k的值为$\sqrt{3}$. 分析 先求得△BOO′是等边三角形,即可求得B的坐标,然后根据待定系数法即可求得双曲线的解析式;
解答 解:(1)∵AB∥x轴,
∴∠ABO=∠BOO′,
∵∠ABO=∠A′BO′,
∴∠BOO′=∠OBO′,
∴OO′=O′B,
∵OB=BO′,
∴△BOO′是等边三角形,
∴∠BOO′=60°,
∵OB=2,
∴B(1,$\sqrt{3}$);
∵双曲线y=$\frac{k}{x}$经过点B,
∴k=1×$\sqrt{3}$=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 本题考查了反比例函数图象上点的坐标特征,旋转的性质,等边三角形的判定和性质,待定系数法求反比例函数的解析式等,求得△BOO′是等边三角形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 买一张电影票,座位号是8 | B. | 射击运动员射击一次,命中10环 | ||
| C. | 明天会下雨 | D. | 度量多边形的外角和,结果是520° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
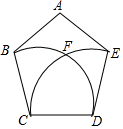 如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则$\widehat{BF}$的长为$\frac{8}{15}$π.
如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则$\widehat{BF}$的长为$\frac{8}{15}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
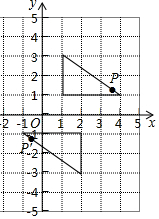 两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )| A. | (b+3,a) | B. | (b,3-a) | C. | (a-3,-b) | D. | (3-a,-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com